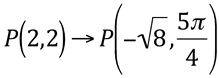O ponto no R2
Coordenadas cartesianas
Dados dois eixos OX e OY, perpendiculares em 0(zero). Eles determinam um plano π. Consideremos um ponto P ∈π e tracemos por ele a reta x’ paralela ao eixo OX e y’ paralela ao eixo OY.
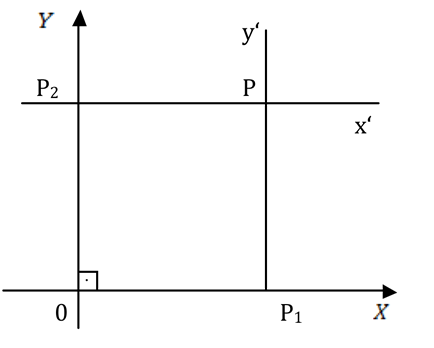
Os pontos P1 e P2 são, respectivamente, as intersecções de y’ com o eixo OX e de x’ com o eixo OY.
0 e o P1 determinam o segmento orientado 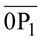 cuja medida algébrica é a abscissa do ponto P.
cuja medida algébrica é a abscissa do ponto P.
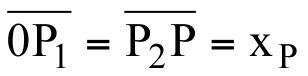
0 e o P2 determinam o segmento orientado 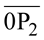 cuja medida algébrica é a ordenada do ponto P.
cuja medida algébrica é a ordenada do ponto P.
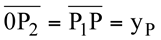
- Os valores de xP e yP constituem um par ordenado ou coordenadas que determinam a posição do ponto P no plano π .
- O plano π é denominado plano cartesiano e os eixos OX e OY são os eixos cartesianos, sendo o eixo OX das abscissas e o eixo OY o eixo das ordenadas.
- XOY indica o sistema de eixos coordenados ortogonais.
- O ponto 0 é a origem do sistema.
Quadrantes
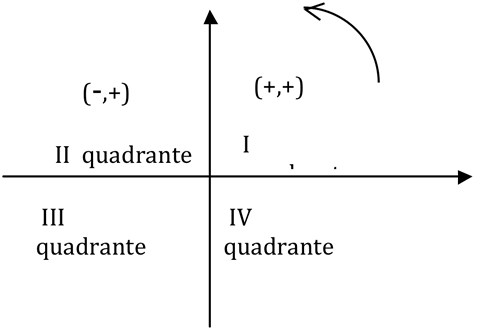
Os eixos coordenados, ao se interceptarem, formam quatro ângulos de 90º, dividindo o plano em quatro regiões denominadas de quadrantes, conforme figura ao lado. Como a intersecção define a origem do plano (0,0), cada quadrante possui uma combinação de sinal distinta. No primeiro quadrante, temos a abscissa e a ordenada positiva, no segundo quadrante, a abscissa negativa e a ordenada positiva, no terceiro quadrante, a abscissa e a ordenada negativa e no quarto quadrante, temos a abscissa positiva e a ordenada negativa. Podemos perceber facilmente que existe uma correspondência biunívoca entre os pontos de um plano cartesiano e pares ordenados (xP,yP) de números reais, ou seja, para cada par ordenado (xP,yP) existe um único ponto P do plano cartesiano correspondente e vice-versa.
Exemplo
Temos seis pontos no plano cartesiano abaixo.
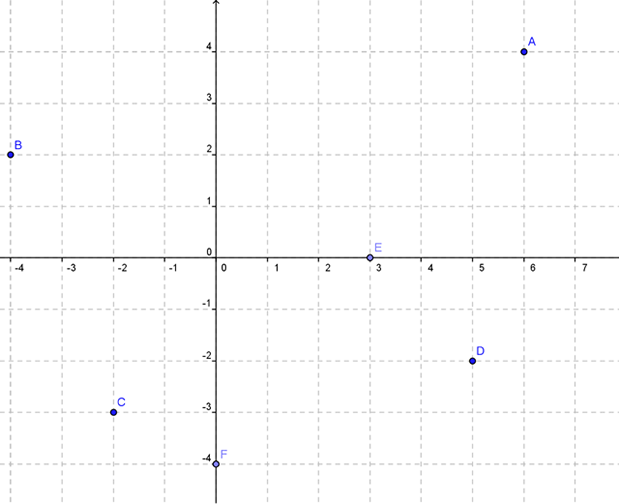
1) O ponto A se encontra no primeiro quadrante com coordenadas A(6,4).
2) O ponto B se encontra no segundo quadrante com coordenadas B(-4,2).
3) O ponto C se encontra no terceiro quadrante com coordenadas C(-2,-3).
4) O ponto D se encontra no quarto quadrante com coordenadas D(5,-2).
5) Já o ponto E pertence ao eixo OX com coordenadas E(3,0).
6) Já o ponto F pertence ao eixo OY com coordenadas F(0,-4).
Note que sempre que um ponto pertence a um dos eixos a coordenada relativa ao outro eixo é nula, ou seja, se o ponto pertence ao eixo OX a ordenada yP=0.
Distância entre dois pontos
Dados os pontos A(xA,yA) e B(xB,yB), a distância d entre esses dois ponto é dado pela seguinte fórmula:
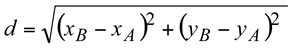
Exemplos
1) Determine a distância entre os pontos A(1,2) e B(3,5).
Solução:
É só substituir os valores das coordenadas na fórmula e fazer as contas:
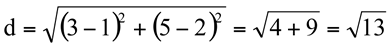
2) Calcule o perímetro do triângulo com os vértices em A(2,3), B(-2,1) e C(2,-3).
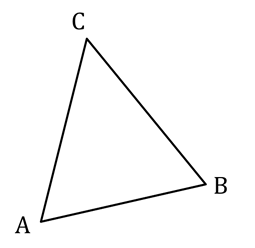
Solução:
Vamos calcular as medidas dos segmentos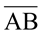 ,
, 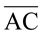 e
e 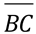 com as distâncias dAB, dAC e dBC, respectivamente.
com as distâncias dAB, dAC e dBC, respectivamente.
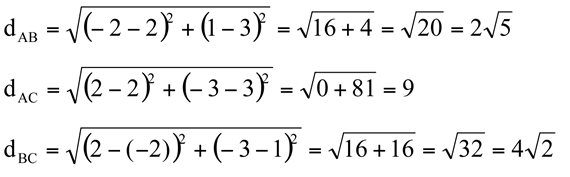
Perímetro=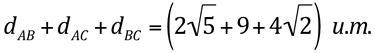
Ponto médio
Dado um segmento orientado 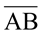 , se C é um ponto médio desse segmento, então suas coordenadas são determinadas pelas médias das coordenadas dos pontos A e B, ou seja,
, se C é um ponto médio desse segmento, então suas coordenadas são determinadas pelas médias das coordenadas dos pontos A e B, ou seja,
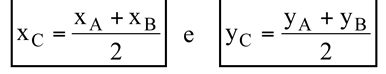
Exemplo
1) Determine as coordenadas do ponto médio do segmento orientado definido pelos pontos A(1,2) e B(3,5).
Resolução:
Substituindo os valores das coordenadas dos pontos A e B nas fórmulas acima, temos:
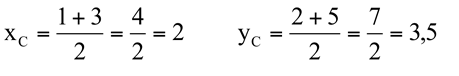
Portanto, o ponto médio é C(2,3,5).
Coordenadas polares
Coordenadas polares é outra forma de representação de um ponto A. A representação se dará pela distância do ponto A até a origem O e essa distância é designada por r e pelo ângulo w que o segmento 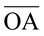 faz com o eixo OX.
faz com o eixo OX.
Considerando uma semirreta OX orientada de um plano. Esta semirreta de origem O (polo), denominado eixo polar, define o sistema polar. Chamamos de coordenadas polares de um ponto A, em relação ao sistema polar dado, aos números 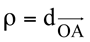 (distância de A até O) e
(distância de A até O) e 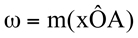 (medida do ângulo que o segmento AO faz com o eixo polar, ou o eixo OX). A notação em coordenadas polares é
(medida do ângulo que o segmento AO faz com o eixo polar, ou o eixo OX). A notação em coordenadas polares é 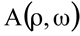 , em que a primeira coordenada ρ é o raio polar e a segunda coordenada ω é o ângulo polar.
, em que a primeira coordenada ρ é o raio polar e a segunda coordenada ω é o ângulo polar.
O ângulo polar ω tem uma infinidade de valores possíveis 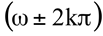 , em que
, em que 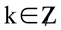 e é contado positivamente no sentido anti-horário. O valor do raio polar ρ (raio vetor) é positivo se estiver no mesmo sentido do terminal do ângulo ω e negativo caso contrário.
e é contado positivamente no sentido anti-horário. O valor do raio polar ρ (raio vetor) é positivo se estiver no mesmo sentido do terminal do ângulo ω e negativo caso contrário.
Um ponto P num plano, em um sistema polar fica bem determinado pela intersecção de uma circunferência de centro em O e raio ρ interseccionado com o semieixo traçado por O e determinado pelo ângulo ω, conforme o exemplo a seguir.
Exemplo
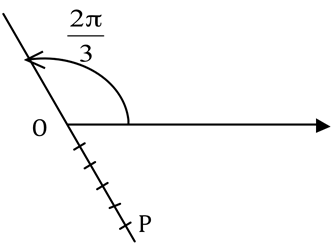
Seja o ponto em coordenadas polares 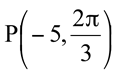 , sua representação se encontra na figura ao lado, em que
, sua representação se encontra na figura ao lado, em que 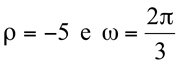 .
.
Usando apenas a menor determinação para ω, podemos representar de 4 formas diferentes o mesmo ponto P.
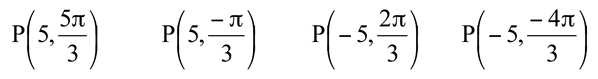
Relação entre coordenadas polares e cartesianas
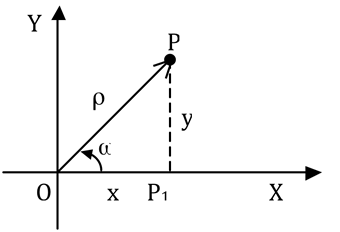
Dado um ponto P representado ao mesmo tempo no sistema cartesiano e no sistema polar. No sistema cartesiano o ponto P tem as coordenadas representadas por x e y e no sistema polar por ρ e ω, ou seja, P(x,y) e P(ρ,ω), respectivamente.
A partir do triângulo retângulo OPP1 podemos tirar as relações:
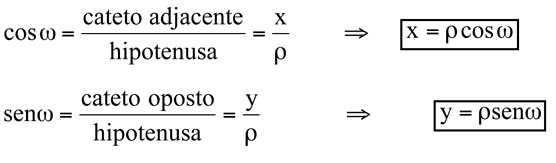
Do mesmo triângulo retângulo, podemos determinar as relações inversas:
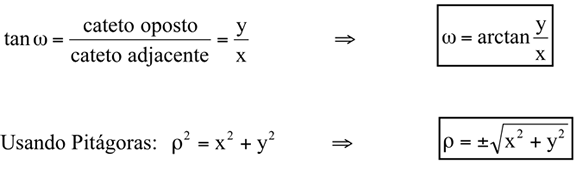
Exemplos
1) Encontre as coordenadas cartesianas do ponto 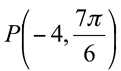
Substituindo 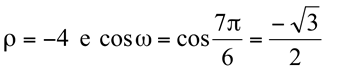 , temos:
, temos:
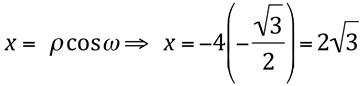
e 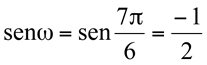 , temos:
, temos:
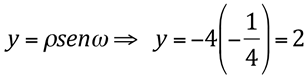
Portanto o ponto P em coordenadas cartesianas é 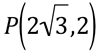 .
.
2) Encontre 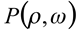 , supondo ρ<0 e
, supondo ρ<0 e 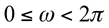 para P(2,2).
para P(2,2).
Substituindo x=2 e y=2 na fórmula 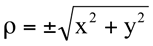 , temos:
, temos:
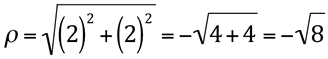
e na fórmula 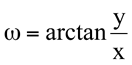 , temos:
, temos:
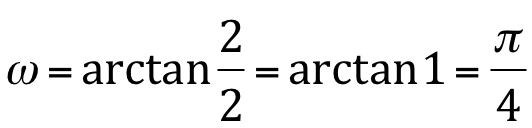
Note que o ponto P se encontra no primeiro quadrante sendo negativo o raio, a medida de ω deve ser 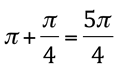 (faça a representação gráfica para verificar).
(faça a representação gráfica para verificar).