O ponto no R3
Coordenadas cartesianas
Tracemos por um ponto fixo O(origem) três eixos perpendiculares entre si conforme figura abaixo.
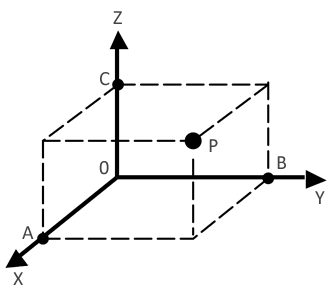
OX → eixo das abscissas
OY → eixo das ordenadas
OZ → eixo das cotas
Os três eixos determinam dois a dois três planos: XOY, XOZ e YOZ.
Dado um ponto P, suas projeções em relação aos eixos coordenados determinam os pontos A, B e C, respectivamente aos eixos OX, OY e OZ.
OA=x (abscissa)
OB=y (ordenada)
OC=z (cota)
Octantes
Vimos que no plano cartesiano os eixos coordenados dividem a região em quatro quadrantes. Como os pontos no espaço são ternas ordenadas e cada eixo possui dois sinais (positivo e negativo), temos oito possíveis combinações de sinais para cada terna ordenada. As oito combinações de sinais situam-se, cada uma, numa região do espaço, denominada de octante.
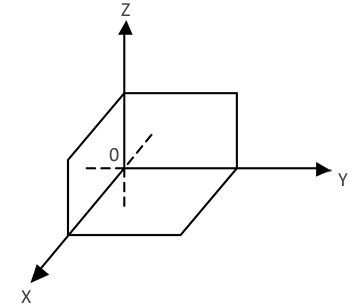
O primeiro octante é aquele que possui todas as coordenadas positivas (veja a figura), depois, em sentido anti-horário, dá-se continuação à contagem dos octantes para z positivo e depois segue a contagem para z negativo.
Caso um ponto pertença a um dos eixos coordenados, será representado por uma terna ordenada com duas componentes nulas. O ponto possuirá as três componentes nulas se, e somente se, esse ponto for a origem. Caso o ponto pertença a um dos planos coordenados, será representado por uma terna com uma componente nula.
Exemplo
Indique em qual octante, ou plano ou eixo coordenado, cada um dos pontos dados está situado:
Pontos: A(2, -4, 8), B(-2, -4, 8), C(2, 4, 8), D(2,- 4, -8), E(-2, 4, -8), F(-2, 4, 8), G(2, 0, 0), H(0, -4, 0), I(0, 0, 8), J(0, -4 ,8), L(2, 0, 8), M(2, -4, 0).
Ponto A: quarto octante
Ponto B: terceiro octante
Ponto C: primeiro octante
Ponto D: oitavo octante
Ponto E: sexto octante
Ponto F: segundo octante
Ponto G: eixo “ox”
Ponto H: eixo “oy”
Ponto I: eixo “oz”
Ponto J: plano “yoz”
Ponto L: plano “xoz”
Ponto M: plano “xoy”
Distância entre dois pontos
Dados os pontos A (XA, YA, ZA) e B (XB, YB, ZB), a distância “d” entre esses dois ponto é: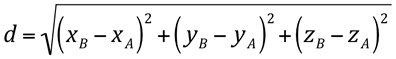 
Exemplos
1) Determine a distância entre os pontos A(-1,2,3) e B(3,-3,4).
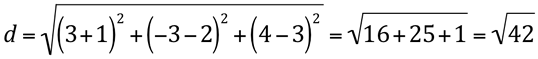
2) Calcule o perímetro do triângulo com os vértices em A(-1,2,3), B(0,-2,1) e C(2,2,-3).
Da mesma forma, como no caso do exemplo do R², calculamos as distâncias dAB, dAC e dBC, respectivamente.
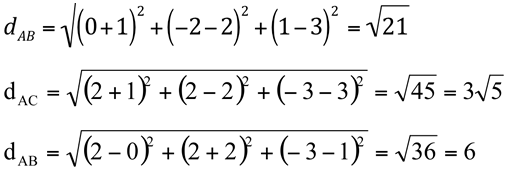
E agora, é só somar as distâncias para obter o perímetro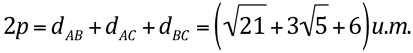 
Ponto médio
Dado um segmento orientado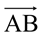 
, se C é um ponto médio desse segmento, então suas coordenadas são determinadas pelas médias das coordenadas dos pontos A e B, ou seja,
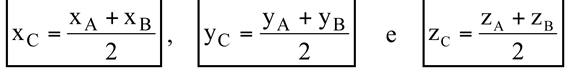
Exemplo
Determine as coordenadas do ponto médio do segmento orientado definido pelos pontos A(3,1,-3) e B(3,7,5).
A solução é só substituir os valores, nas fórmulas acima, temos:
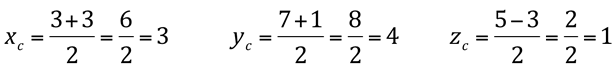
Portanto, o ponto médio é C (3,4,1).