Definição de Vetor
Pela definição de segmentos equipolentes, podemos concluir que existem infinitos segmentos equipolentes a outro previamente definido. A esse conjunto de infinitos segmentos equipolentes, damos o nome de vetor.
Definição de vetor
Vetor é um conjunto de segmentos equipolentes a outro segmento previamente definido. Se definirmos um segmento ![]() , ao conjunto de todos os segmentos equipolentes à
, ao conjunto de todos os segmentos equipolentes à ![]() , chamaremos de vetor determinado por
, chamaremos de vetor determinado por ![]() e indicaremos por
e indicaremos por ![]() .
.
Podemos, ainda, indicar um vetor qualquer por letras minúsculas do nosso alfabeto latino, quando não se tratar de nenhum segmento em especial.
Obs.: O nome vetor se dá por ser elemento de um espaço vetorial. A definição de espaço vetorial será vista mais adiante.

Um vetor ![]() sempre será caracterizado por sua direção, seu sentido e seu módulo que indicaremos por |
sempre será caracterizado por sua direção, seu sentido e seu módulo que indicaremos por |![]() |.
|.
Se considerarmos um vetor ![]() e um ponto
e um ponto ![]() (origem do vetor) qualquer do espaço, existirá um único segmento orientado
(origem do vetor) qualquer do espaço, existirá um único segmento orientado ![]() representante de
representante de ![]() e poderemos escrever
e poderemos escrever ![]() .
.
Definição de vetor nulo
Um vetor é nulo quando seu representante for um segmento orientado nulo, ou seja, quando a origem e a extremidade do segmento coincidirem. Indicaremos esse vetor por ![]() .
.
Definição de vetor oposto
Um vetor ![]() é dito oposto de
é dito oposto de ![]() quando a origem de
quando a origem de ![]() for a extremidade de
for a extremidade de ![]() e a extremidade de
e a extremidade de ![]() for a origem de
for a origem de ![]() . Se
. Se ![]() for definido pelo segmento
for definido pelo segmento ![]() , ou seja, se
, ou seja, se ![]() e se
e se ![]() for o oposto de
for o oposto de ![]() , teremos
, teremos ![]() .
.

Definição de vetores iguais
Dois vetores serão iguais se possuírem mesma direção, mesmo sentido e mesmo módulo. Podemos ter vetores iguais sobre a mesma reta ou sobre retas paralelas.
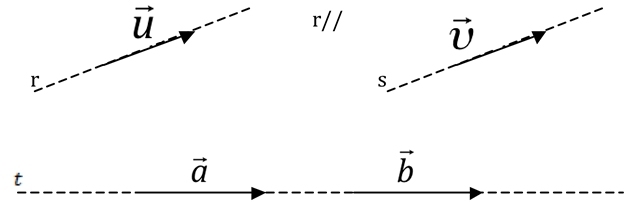
Definição de vetor unitário
Um vetor ![]() é unitário se
é unitário se ![]() .
.
Definição de versor
Um versor é um vetor que possui mesma direção e mesmo sentido que outro vetor, porém, possui uma unidade de comprimento. Em outras palavras: se ![]() é versor de
é versor de ![]() , então
, então ![]() possui mesma direção e mesmo sentido que
possui mesma direção e mesmo sentido que ![]() e, além disso,
e, além disso, ![]() . Só faz sentido falarmos em versor quando referenciarmos um vetor ao qual queremos tomar seu versor.
. Só faz sentido falarmos em versor quando referenciarmos um vetor ao qual queremos tomar seu versor.

Definição de módulo de um vetor
Estabelecida uma unidade de medida, é possível medir o módulo, norma ou comprimento de um vetor que será o mesmo de qualquer um de seus representantes.

Operações com vetores
- a) Soma de vetores
A soma de dois vetores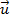 e
e 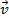 quaisquer resultam num vetor que indicaremos por
quaisquer resultam num vetor que indicaremos por 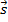 e que é dado por
e que é dado por 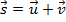 . Geometricamente, representaremos o vetor
. Geometricamente, representaremos o vetor 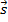 da seguinte forma:
da seguinte forma:

Se o vetor
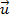 for o representante do segmento
for o representante do segmento 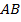 (
(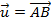 ) e o vetor
) e o vetor 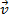 for o representante do segmento
for o representante do segmento 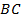 (
(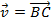 ), então o vetor
), então o vetor 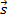 será o representante do segmento
será o representante do segmento 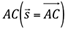 , ou seja,
, ou seja, 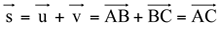 .
.

Ou, como já vimos que podemos representar um vetor por qualquer outro equipolente a ele, podemos tomar um vetor equipolente ao vetor
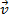 , com origem coincidindo com a do vetor
, com origem coincidindo com a do vetor 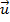 e teremos assim o vetor
e teremos assim o vetor 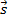 representando a maior diagonal do paralelogramo formado por
representando a maior diagonal do paralelogramo formado por 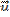 e
e 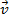 .
.
Propriedades da soma de vetores
Sejam
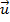 ,
, 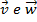 três vetores quaisquer.
três vetores quaisquer.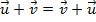 (comutatividade).
(comutatividade).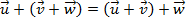 (associatividade).
(associatividade).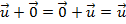 (elemento neutro).
(elemento neutro).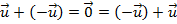 (elemento simétrico)
(elemento simétrico)
Faremos a demonstração da segunda e da quarta propriedade, as demais ficam a cargo do leitor.
ii. Supondo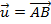 ,
, 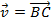 e
e 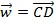
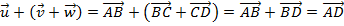
Por outro lado,
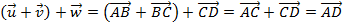
iv. Supondo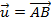 , por definição de vetor oposto, temos
, por definição de vetor oposto, temos 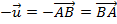 , logo:
, logo:
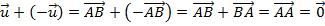
E se valendo da propriedade i (comutatividade),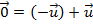 .
.
- b) Diferença de vetores
A diferença de dois vetores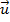 e
e 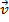 quaisquer resultam num vetor
quaisquer resultam num vetor 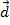 que indicaremos por
que indicaremos por 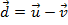 . Geometricamente, representaremos o vetor
. Geometricamente, representaremos o vetor 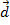 da seguinte forma:
da seguinte forma:
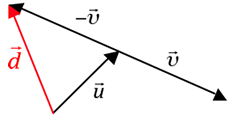
Sabemos que, por definição, um vetor oposto ao vetor
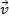 tem mesma direção, mesmo módulo e sentido contrário a
tem mesma direção, mesmo módulo e sentido contrário a 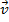 , sendo designado por
, sendo designado por 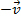 .
.Podemos reescrever a igualdade
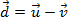 como uma soma de vetores:
como uma soma de vetores: 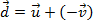 . Dessa forma, damos o mesmo tratamento da soma para a diferença.
. Dessa forma, damos o mesmo tratamento da soma para a diferença. Se representarmos o vetor
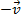 por outro equipolente a ele, com origem coincidindo com a do vetor
por outro equipolente a ele, com origem coincidindo com a do vetor 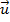 , obteremos o vetor
, obteremos o vetor 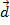 representando a maior diagonal do paralelogramo formado por
representando a maior diagonal do paralelogramo formado por 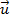 e
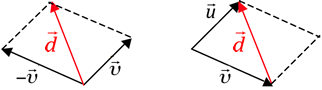
e 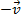 ou, ainda, podemos considerá-lo como a menor diagonal do paralelogramo formado por
ou, ainda, podemos considerá-lo como a menor diagonal do paralelogramo formado por 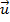 e
e 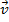 .
.
Se o vetor
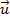 for o representante do segmento
for o representante do segmento 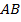 (
(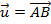 ), o vetor
), o vetor 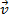 representante do segmento
representante do segmento 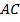 (
(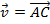 ), então o vetor
), então o vetor 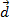 será o representante do segmento
será o representante do segmento 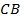 (
(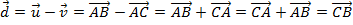 ).
).
Note que: (vetor oposto) e
(vetor oposto) e 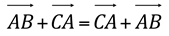 (comutatividade).
(comutatividade).
Como a diferença é um caso particular da soma, valem as mesmas propriedades. - c) Multiplicação de um número real por um vetor
Ao multiplicarmos um vetor
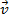 qualquer por um número real
qualquer por um número real 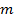 , obteremos como resultante um vetor e o indicaremos por
, obteremos como resultante um vetor e o indicaremos por 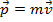 . Caso
. Caso 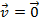 ou
ou 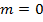 ,
, 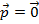 . Se
. Se 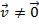 e
e 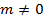 , então:
, então:- Se
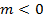 : nesse caso o vetor
: nesse caso o vetor 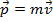 terá mesma direção que
terá mesma direção que 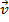 porém sentido contrário.
porém sentido contrário. - Se ainda
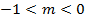 ,
, 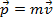 terá módulo menor que
terá módulo menor que 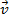 e se
e se 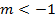 ,
, 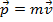 terá módulo maior que
terá módulo maior que 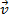 .
.
- Se
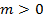 : nesse caso o vetor
: nesse caso o vetor 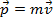 terá mesma direção e mesmo sentido que
terá mesma direção e mesmo sentido que 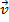 .
.
- Se ainda
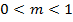 ,
, 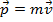 terá módulo menor que
terá módulo menor que 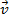 e se
e se 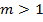 ,
, 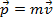 terá módulo maior que
terá módulo maior que 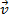 .
.
- Se ainda
- Se
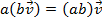 (comutatividade)
(comutatividade)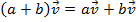 (distributividade em relação à adição de escalares)
(distributividade em relação à adição de escalares)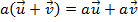 (distributividade em relação à adição de vetores)
(distributividade em relação à adição de vetores)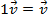 (identidade)
(identidade)
 |  | |
|
Resumindo: | ||
 |  |
Obs.: Ao multiplicarmos um vetor por um número real (um escalar), a direção do vetor não se altera.
Exemplos:
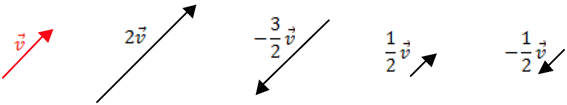
Propriedades da multiplicação de um número real por um vetor
Sejam ![]() e
e ![]() dois vetores quaisquer e
dois vetores quaisquer e ![]() e
e ![]() dois números reais quaisquer:
dois números reais quaisquer:
Faremos apenas a demonstração da quarta propriedade.
Se ![]() então
então ![]() por definição.
por definição.
Se ![]() , então
, então ![]() possui mesmo sentido que
possui mesmo sentido que ![]() , pois nesse caso
, pois nesse caso ![]() e ainda
e ainda ![]() o que indica que
o que indica que ![]() e
e ![]() tem o mesmo módulo. Como sabemos que na multiplicação por escalar a direção do vetor não é alterada, podemos concluir que
tem o mesmo módulo. Como sabemos que na multiplicação por escalar a direção do vetor não é alterada, podemos concluir que ![]() .
.
Vetores colineares
Dois vetores são ditos colineares se possuírem mesma direção, independentemente de seu módulo e sentido. Para que dois vetores sejam colineares, eles devem pertencer à mesma reta suporte ou a retas paralelas.
Como vimos que na multiplicação por escalar a direção se mantém, o vetor ![]() é colinear ao vetor
é colinear ao vetor ![]() .
.
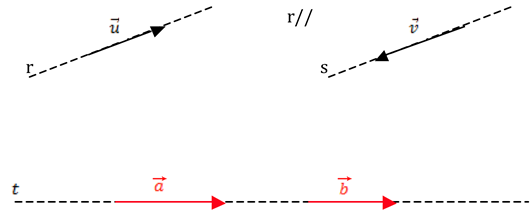
Neste caso, ![]() é colinear a
é colinear a ![]() e
e ![]() é colinear a
é colinear a ![]() .
.