Vetores no R²
Dados dois pontos 
e 
quaisquer do plano, podemos definir um vetor representante do segmento 
.
Convencionaremos, no plano cartesiano, o vetor representante do segmento 
como o vetor que possui origem na origem do sistema cartesiano (no ponto 
) e indicaremos 
.
Os pontos 
e 
são representados por pares ordenados 
e 
.
Sendo assim, 
.
Representação analítica de um vetor no plano
Representamos, analiticamente, um vetor no plano por 
, onde o par ordenado 
é a extremidade do vetor que possui origem na origem do sistema de coordenadas cartesianas.
Exemplo:
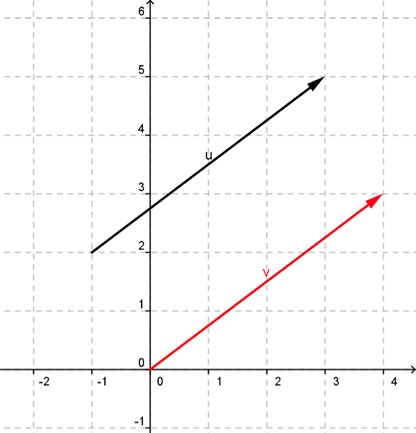
Neste exemplo, temos o vetor 
representante do segmento 
com 
e 
e o vetor 
, equipolente ao vetor 
, com origem no ponto 
e extremidade no ponto
.
Decomposição de um vetor no plano
Um vetor 
do plano pode ser decomposto segundo as direções de dois vetores 
e 
não colineares. Em outras palavras, podemos sempre escrever um vetor como sendo a soma de dois vetores não colineares previamente multiplicados por escalares reais.
Exemplo:
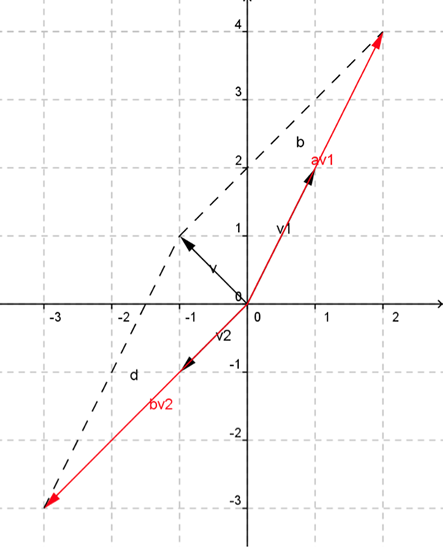
O vetor pode ser decomposto segundo as direções de 
e de 
da seguinte forma: 
. Nesse caso, dizemos que 
é uma combinação linear de 
e 
(Você verá essa definição com maiores detalhes na unidade que trata de bases de espaços vetoriais).
Como 
e 
são dois vetores não colineares, qualquer vetor do plano pode ser decomposto segundo suas direções, bastando para isso, encontrar os escalares 
e 
tais que 
. Dizemos que 
e 
formam uma base para o plano.
Nessa unidade, trataremos de uma base em particular, a base canônica do 
composta pelos vetores 
e 
que são ortonormais, isto é, são ortogonais e, além disso, 
, ou seja, são unitários.
Podemos escrever qualquer vetor do plano como combinação linear de
e 
: 
Exemplos:
Operações com vetores no R²
- a) Igualdade de vetores
Dois vetores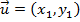
e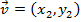 
são iguais se, e somente se, 
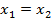e 
.
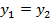Exemplo: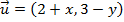
e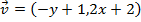 
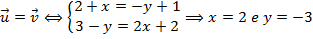
- Soma de vetores no R²
Sejam os vetores
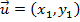e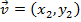 
. Define-se a soma de 
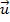com 
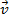por: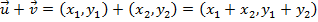
Exemplo:S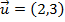e
e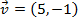 
, então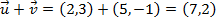 
- c) Multiplicação de um número real por um vetor
Seja o vetor
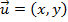e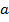 
um número real qualquer. Define-se a multiplicação de um número real por um vetor como sendo: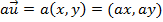
Exemplo:
Se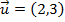
e 
, então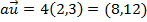 
Módulo de um vetor no R²
Seja 
um vetor não nulo do 
.
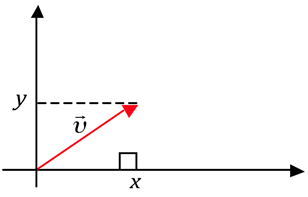
Considerando que todo vetor pode ser representado como a diagonal de um paralelogramo de lados 
e 
, podemos calcular o seu módulo com a ajuda do teorema de Pitágoras: 
Ou ainda, 
Cálculo do versor
Como vimos o versor de um vetor 
possui mesma direção e sentido de 
, porém é unitário.
- Se um vetor tiver módulo igual a 3 unidades de medida, ao dividi-lo por 3, ou multiplicá-lo por 1/3 , obteremos um vetor de módulo 1, de mesma direção e sentido.
- Se um vetor tiver módulo igual a 5 unidades de medida, ao dividi-lo por 5, ou multiplicá-lo por 1/5 , obteremos um vetor de módulo 1, de mesma direção e sentido.
- Seguindo esse raciocínio, se dividirmos um vetor por seu módulo, obteremos um vetor unitário, de mesma direção e mesmo sentido já que o módulo é sempre um valor positivo, logo:
Exemplo:
O versor do vetor 
é o vetor 
já que 
.