Vetores no R³
Dados dois pontos 
e 
quaisquer do espaço cartesiano 
, podemos definir um vetor representante do segmento 
ao vetor que possui extremidade em B e origem em A e indicaremos por 
.
Os pontos 
e 
são representados por ternas ordenadas 
e 
. Sendo assim, 
.
Representação analítica de um vetor no espaço
Representamos, analiticamente, um vetor no espaço por 
, onde a terna ordenada 
é a extremidade do vetor que possui origem na origem do sistema de coordenadas cartesianas.
Exemplo:
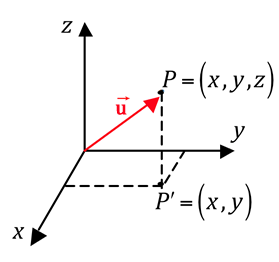
Neste exemplo, temos o vetor 
representante do segmento 
que possui origem na origem do espaço e extremidade no ponto 
.
Para representar, geometricamente, esse vetor, podemos utilizar o seguinte procedimento: marcamos o par ordenado 
no plano e em seguida, a partir de 
, subimos ou descemos “
” unidades, dependendo do sinal positivo ou negativo de “z”, respectivamente.
Podemos ainda, pensar da seguinte forma: considere que para marcar a extremidade de um vetor, você deve partir sempre da origem 
. Considere ainda que a terna ordenada 
é um comando que você deve seguir. O valor de 
é o comando que manda você se deslocar no sentido positivo ou negativo (conforme for o sinal de 
) do eixo 
, em 
unidades. O valor de 
é o comando que manda você se deslocar no sentido positivo ou negativo (conforme for o sinal de 
) do eixo 
, em 
unidades. E finalmente, o valor de 
é o comando que manda você se deslocar no sentido positivo ou negativo (conforme for o sinal de 
) do eixo 
, em z unidades.
Exemplo:
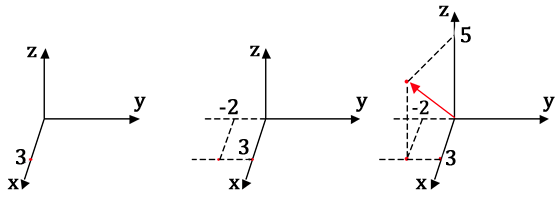
Seja 
. Para representá-lo graficamente, é preciso representar o ponto 
e traçar o vetor 
. Considere o ponto 
como o comando: a partir da origem, desloque-se em três unidades no sentido positivo do eixo 
. Em seguida, a partir da nova posição, desloque-se em duas unidades no sentido negativo do eixo 
. Finalmente, desloque-se em cinco unidades no sentido positivo do eixo 
.
Decomposição de um vetor no espaço
Um vetor 
do espaço pode ser decomposto segundo as direções de três vetores 
, 
e 
não coplanares (vetores coplanares são aqueles que estão no mesmo plano). Em outras palavras, podemos sempre escrever um vetor como sendo a soma de três vetores não coplanares, previamente multiplicados por escalares reais.
Exemplo:
O vetor 
pode ser decomposto segundo as direções de 
, de 
e de 
, da seguinte forma: 
. Nesse caso, dizemos que 
é uma combinação linear de 
, 
e 
Como 
, 
e 
são três vetores não coplanares, qualquer vetor do espaço pode ser decomposto segundo suas direções, bastando para isso, encontrar os escalares 
, 
e 
tais que 
. Dizemos que 
, 
e 
formam uma base para o espaço.
Podemos escrever qualquer vetor do espaço como combinação linear de 
, 
e 
: 
.
Exemplos:
Operações com vetores no R³
- a) Igualdade de vetores
Dois vetores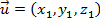
e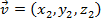 
são iguais se, e somente se, 
, 
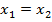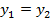e 
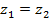. - Exemplo:
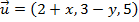e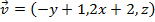 
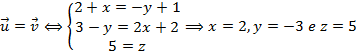
- b) Soma de vetores no
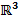
Sejam os vetores
, 
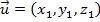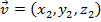e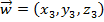 
. Define-se a soma de 
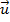com 
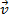por: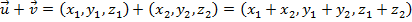
. - Exemplo:
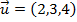Se
e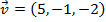 
, então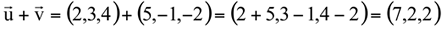
- c) Multiplicação de um número real por um vetor
Sejam o vetor
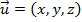e o escalar 
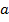um número real qualquer. Define-se a multiplicação de um número real por um vetor como sendo: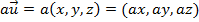
Exemplo:
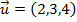Se
e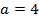 
, então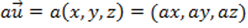 
Módulo de um vetor no R³
Seja 
um vetor não nulo do 
.
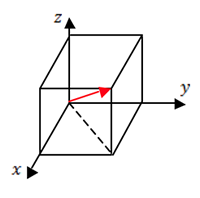
Considerando que todo vetor do espaço pode ser representado como a diagonal de um paralelepípedo de lados 
, 
e 
, podemos calcular o seu módulo com a ajuda do teorema de Pitágoras: 
Ou ainda, 
Exemplo:
Calcule o módulo de 
.
