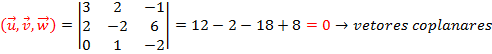Operações com vetores
Produto escalar entre dois vetores
Define-se o produto escalar entre os vetores 
e 
, e anota-se por 
ou 
, o escalar assim obtido:
Sejam os vetores 
e 
:
- A definição também é válida para vetores no plano.
Ângulo entre dois vetores
O ângulo 
entre os vetores 
e 
é assim calculado:
Demonstração:
Utilizaremos a Lei dos Cossenos para realizar essa demonstração:
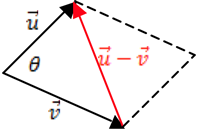
Considerando que
, então
Co-senos diretores
Chamamos de co-senos diretores, os cossenos dos ângulos formados por um vetor e os vetores da base canônica. Os ângulos formados são os ângulos diretores.
Sejam 
, 
e 
os ângulos formados entre o vetor 
e os vetores 
, 
e 
respectivamente, então:
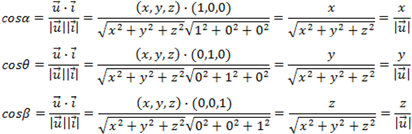
Note que 
.
Condição de ortogonalidade entre dois vetores: 
Dois vetores ortogonais possuem ângulo de 90o.
Sabemos que 
, logo:
Condição de paralelismo entre dois vetores: 
Dois vetores são paralelos se possuem mesma direção, o que nos leva à definição de vetores colineares, ou seja, se dois vetores são paralelos então são colineares.
Já vimos que se 
e 
são colineares, temos: 
, 
.
Fazendo 
e 
e desenvolvendo a equação acima, temos:
Pela definição de igualdade vem:
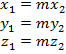
Isolando 
em todas as equações, no caso de serem todas não nulas as coordenadas de 
, temos:
Caso alguma coordenada de 
seja nula, os vetores só serão paralelos se a coordenada correspondente em 
também for nula.
Exemplos:
e 
são paralelos, pois 
.
e 
são paralelos, pois 
.
e 
não são paralelos, pois 
.
Produto vetorial
Sejam 
e 
dois vetores quaisquer do 
. Definimos produto vetorial e representamos por 
, o vetor obtido da seguinte operação:
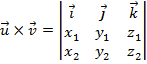
Exemplo:
Sejam os vetores 
e 
. Determinar o produto vetorial 
.
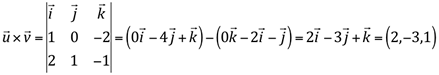
Atenção: o resultado do produto vetorial é um vetor!
Propriedades do produto vetorial
As cinco primeiras propriedades do produto vetorial decorrem das propriedades do determinante, as demais podem ser verificadas desenvolvendo os dois lados da igualdade. Fica a cargo do leitor demonstrá-las.
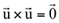
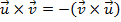
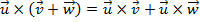
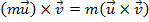
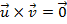se, e somente se, um dos vetores for nulo ou s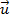e 
e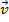 
forem colineares.- (
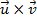) é ortogonal a 
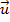e também a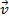 
(
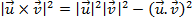
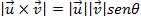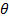é o ângulo entr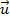e 
e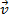 
, ambos não nulos)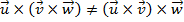
Módulo do produto vetorial
Considere o paralelogramo formado por dois vetores 
e 
.
Vamos calcular sua área:
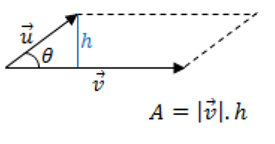
Da trigonometria vem que 
.
Substituindo 
na equação acima temos: 
E pela propriedade viii, 
O módulo do produto vetorial entre dois vetores 
e 
resulta na área do paralelogramo formado por 
e 
.
Produto misto
Define-se produto misto entre três vetores 
, 
e 
do 
e representa-se por 
, o número real 
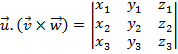
Propriedades do produto misto
As propriedades do produto misto decorrem das propriedades do determinante. Fica a cargo do leitor demonstrá-las.
- Quando dois vetores são colineares ou quando um deles é nulo ou ainda, quando os três vetores são coplanares (estão no mesmo plano), então
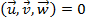
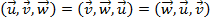Se trocarmos todas as linhas numa ordem circular, o resultado do produto misto se mantém.
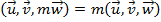Ao multiplicarmos um vetor por um escalar real, o resultado do produto misto fica multiplicado pelo mesmo escalar real.
.
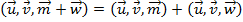Interpretação geométrica do produto misto
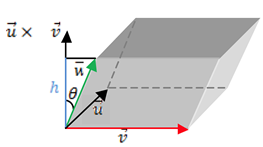
O módulo do produto misto resulta no volume do paralelepípedo gerado pelos três vetores. Caso os três vetores sejam coplanares, o resultado do produto misto é nulo.
Considere o paralelepípedo formado por três vetores 
, 
e 
. Vamos calcular seu volume:
Mas 
Fazendo a substituição temos:
ou ainda (consideramos 
pois 
pode ser obtuso).
Sabemos ainda, do cosseno do ângulo entre dois vetores, que: 
Logo: 
Obs.: Da primeira propriedade do produto misto, temos a condição para que três vetores sejam coplanares: 
Exemplo:
Verifique se os vetores 
, 
e 
são coplanares.
Para isso calculamos o produto misto 
