Posições relativas de duas retas
Duas retas podem ser coplanares (contidas no mesmo plano) ou reversas (em planos diferentes).
Retas coplanares
Neste caso, temos três situações possíveis:
- As retas são concorrentes: são retas que se interceptam num único ponto e temos
. - As retas são paralelas: não há intersecção e temos
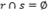
- As retas são coincidentes: as retas possuem todos os pontos em comum e temos
.
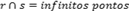Em qualquer um dos casos acima, temos retas coplanares o que nos garante a condição de coplanaridade entre duas retas.
Se a condição de coplanaridade for satisfeita e ainda, se os vetores diretores forem colineares, teremos um caso de paralelismo ou de coincidência. Se for um caso de coincidência, teremos pontos em comum o que é fácil de verificar, bastando para isso tomar um ponto de uma das retas e ver se pertence também à outra. Caso isso não aconteça, sabemos que o caso é de paralelismo.
Se ainda, sabendo que as retas são coplanares, os vetores diretores não forem colineares, teremos um caso de concorrência.
Retas não coplanares
As retas não coplanares são denominadas de reversas. São retas que não possuem pontos de intersecção e por pertencerem a planos distintos, o produto misto da condição de coplanaridade não é nulo.
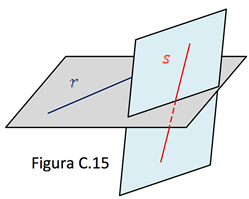Se 
então r e s são reversas.
Para estudar a posição relativa entre duas retas, você pode seguir os seguintes passos:
- Tome um ponto de cada reta, gerando o vetor
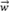que possui origem numa das retas e extremidade na outra e juntamente com os vetores diretores, calcule o produto misto. - Se o resultado do produto misto for nulo, as retas poderão ser concorrentes, paralelas ou coincidentes.
- Analise as direções dos vetores diretores. Se forem colineares, as retas serão paralelas ou coincidentes.
- Se forem coincidentes, qualquer ponto que pertença a uma reta, pertencerá também à outra. Se não forem coincidentes, serão paralelas.
- Se o resultado do produto misto for não nulo, as retas serão reversas.
Veja o esquema abaixo:
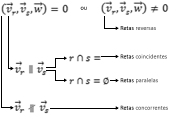
Exemplo
Verifique a posição relativa entre as retas r e s.
a) 
b) 
Solução:
a) 
São vetores colineares o que significa que as retas ou são paralelas ou são coincidentes. Neste caso, nem é preciso calcular o produto misto, pois sabemos que se duas linhas de um determinante são proporcionais, o resultado é nulo.
Vamos agora escolher um ponto da reta r e verificar se esse ponto também pertence à reta s.
Atribuindo z = 0 e substituindo na reta S, temos x = 1 e y = 4 (o que dá o ponto 
. Logo, o ponto 
e concluímos que as retas são paralelas.
b) 
Como os vetores diretores não são colineares, vamos definir o vetor e calcular o produto misto 
.
Logo, as retas são reversas.