Reta ortogonal a duas retas
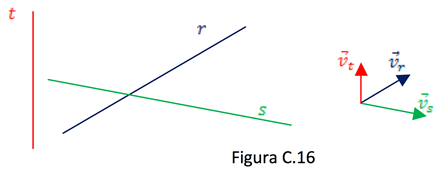
Para que uma reta t seja ortogonal a duas outras retas r es não colineares, basta que seu vetor diretor seja ortogonal, simultaneamente, aos vetores de r e de s.
Vimos, na unidade anterior, que o produto vetorial entre dois vetores 
e 
, gera um vetor 
, simultaneamente ortogonal a e a .
Sendo assim, podemos tomar para 
qualquer múltiplo de 
.
Exemplo
Queremos equacionar uma reta t que seja ortogonal às retas r es dadas e que passe pelo ponto P(-3, 0, 2).
Logo, a reta t terá como vetor diretor o vetor 
e, como passa no pelo ponto P(-3, 0, 2), terá suas equações dadas por:
