Equação vetorial da reta
Que elementos são necessários para definirmos uma reta? Basta um ponto? Basta um vetor?
Pense num ponto. Por esse ponto que você pensou, podemos traçar infinitas retas que se interceptam nesse ponto. Pense num vetor. Com a direção do vetor que você pensou, podemos ter infinitas retas que serão paralelas. Agora, se tomarmos um ponto e um vetor, aí, sim, poderemos definir uma reta.
Uma reta fica bem definida se conhecermos sua direção e um ponto que pertença a ela.
Considere uma reta r que terá a direção de um vetor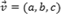 
e que conterá o ponto A(x0, y0, z0). Ao vetor
que indica a direção da reta, daremos o nome de vetor diretor da reta r.Veja as figuras.
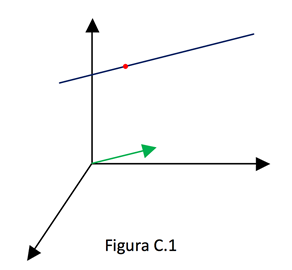
Na figura C.1, temos uma reta que passa pelo ponto A e tem a direção do vetor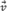 
.
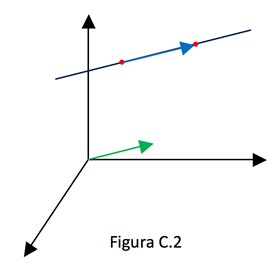
Se considerarmos, sobre a reta r, um ponto qualquer P(x, y, z), o vetor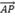 
que representa o segmento orientado AP será paralelo ao vetor 
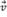. (ver figura C.2)
Pela condição de paralelismo de dois vetores, podemos escrever:
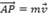, com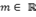 
.
Fazendo as devidas substituições, temos:
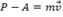ou ainda,
(x, y, z) - (x0, y0, z0) = m(a,b,c), isolando o ponto P temos a equação vetorial da reta r.
(x, y, z) = (x0, y0, z0) + m(a,b,c).
Exemplo
A equação vetorial da reta que passa pelo P(3, -2, 1) e possui a direção do vetor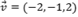 
é:
(x, y, z) = (3, -2, 1) + m(-2, -1, 2)
Se fizermos m variar no conjunto dos números reais, obteremos todos os pontos sobre a reta r.
Se m = 2, por exemplo, então teremos o ponto P(-1, -4, 5), já que (x, y ,z) = (3, -2, 1) + 2(-2, -1, 2) = (-1, -4, 5).