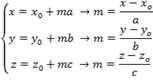Equações simétricas da reta
Agora vamos supor que o vetor diretor 
possua todas as suas componentes não nulas.
Se isolarmos m nas equações paramétricas, teremos:
Como o valor de m é o mesmo para as três equações, podemos dizer que:
Essas equações são chamadas de Equações simétricas da reta r.
Exemplo
As equações simétricas da reta que passa pelo P(3, -2, 1) e possui a direção do vetor 
são:
Se, das equações simétricas, trabalharmos as igualdades, uma de cada vez, de modo a isolarmos uma variável em função da outra, obtendo duas equações, y em função de x e z em função de x por exemplo, teremos, por fim, as Equações reduzidas da reta r.
Vamos trabalhar com a seguinte equação:
Vamos isolar a variável y:
Note que as únicas variáveis da equação são x e y.
Se substituirmos 
por m e 
por n, teremos: y = mx + n.
Assim, deixamos y em função de x. Agora façamos o mesmo para deixarmos z em função de x:
Note que as únicas variáveis da equação são x e z.
Se substituirmos 
por p e 
por q, teremos: z = px + q.
O sistema formado por essas duas equações é chamado de equações reduzidas em x. Se isolarmos as variáveis em função de y ou de z, teremos as equações reduzidas em y ou as equações reduzidas em z.
Exemplo
Quais são as equações reduzidas em x da reta que passa pelo ponto P(3, -2, 1) e possui a direção do vetor 
?
Considerando as equações simétricas do exemplo anterior, temos:
podemos trabalhar as equações para isolar y e z, obtendo
Note que nas equações paramétricas, o vetor diretor da reta fica bem explícito nos coeficientes de m. Nas equações simétricas, as componentes do vetor diretor estão nos denominadores e nas equações reduzidas você pode identificar o vetor diretor, isolando a variável independente, e teremos 
, 
ou 
conforme as equações forem reduzidas em x, y ou z, respectivamente.