Unidade C – A RETA NO IR³

Retas paralelas aos planos e aos eixos

Retas paralelas aos planos

Se as componentes do vetor diretor possuem uma ou duas coordenadas nulas, teremos os casos especiais em que as retas serão para­lelas aos planos ou aos eixos coordenados.

Consideremos, primeiro, que uma das componentes do vetor diretor é nula.

• 

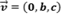
  Nesse caso, as equações da reta ficam:

  

  

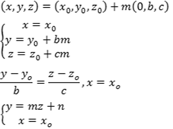
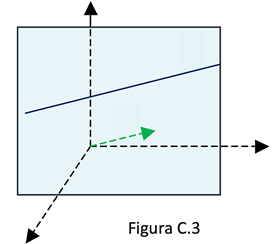
  Essa reta é paralela ao plano "yoz"  já que a variável x é uma constante, variando apenas y e z.

• 

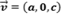
  Nesse caso, as equações da reta ficam:

  

  

  

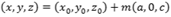
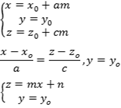
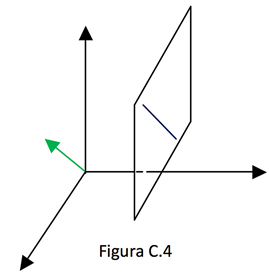
  Essa reta é paralela ao plano "xoz" já que a variável y é uma constante, variando apenas x e z.

• 

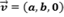
Nesse caso, as equações da reta ficam:





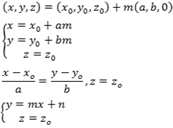
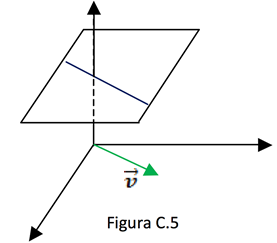
Essa reta é paralela ao plano "xoy" já que a variável z é uma constante, variando apenas x e y.

Exemplos

Verifique que a reta r é paralela ao plano "xoy".



Se a reta é paralela ao plano "xoy", então seu vetor diretor deve formar um ângulo de 90º com o eixo "oz", já que qualquer vetor do plano "xoy" é perpendicular ao eixo "oz".

O vetor diretor de r é  e como vetor diretor do eixo "oz" podemos considerar o vetor . Fazendo o produto escalar entre  e  obtemos zero como resultado, o que garante a ortogonalidade entre esses vetores, ou seja, a reta r é paralela ao plano "xoy".

Determine as equações paramétricas da reta S, paralela ao plano "xoz" e que passa pelo ponto A(1, 4, -2). Sabe-se ainda que a reta S é perpendicular ao vetor .

Se a reta é paralela ao plano "xoz", então seu vetor diretor deve ser ortogonal ao vetor diretor do eixo "oy" já que o plano "xoz"é perpendicular ao eixo "oy". Como a reta ainda é perpendicular a outro vetor, seu vetor diretor também deverá ser ortogonal a esse vetor.

Vimos na unidade anterior, que o produto vetorial entre  e  nos garante um vetor simultaneamente ortogonal a  e a . Nesse caso, o vetor diretor da reta S é um vetor simultaneamente ortogonal ao vetor  (já que esse vetor pertence ao eixo "oy") e ao vetor .

Fazendo o produto vetorial entre  e , temos:



Assim, as equações paramétricas de S são:

Retas paralelas aos eixos

• 

Se uma reta é paralela ao eixo "ox", então seu vetor diretor é paralelo ao vetor.

Suas equações são:



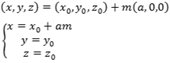
ou





• 

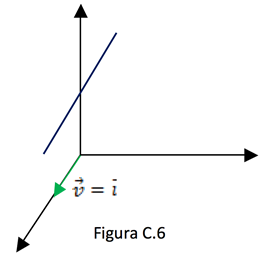
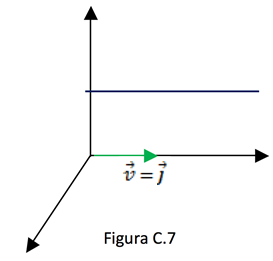
Se uma reta é paralela ao eixo "oy", então seu vetor diretor é paralelo ao vetor: .

Suas equações são:



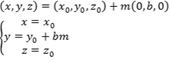
ou





• 

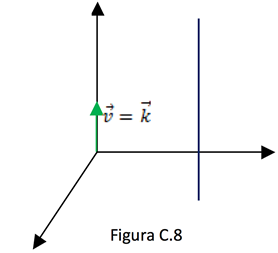
Se uma reta é paralela ao eixo "oz", então seu vetor diretor é paralelo ao vetor .

Suas equações são:



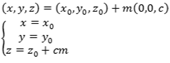
ou





Exemplos

Determine as equações da reta r paralela ao eixo "oz"  e que passa pelo ponto A(3, 1, 2).

Sabemos que apenas os valores de z irão variar e que x e y são fixos em 3 e 1 respectivamente. Assim,

Determine as equações da reta S, paralela ao eixo "ox" e que passa pela origem.

Nesse caso, temos o próprio eixo "ox" que possui equação