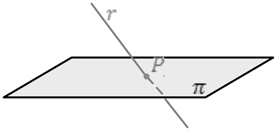
Intersecção de reta e plano
Se uma reta intercepta um plano, existe um ponto em comum entre a reta e o plano.
Uma maneira simples de verificar se existe essa intersecção é escrever as equações reduzidas da reta e substituir as variáveis dependentes na equação do plano. O resultado encontrado nessa equação será o valor de uma das componentes do ponto de intersecção, se este existir. Depois, substituímos esse valor nas outras equações da reta para calcular as outras componentes. Não haverá intersecção no caso de paralelismo entre reta e plano.
Exemplo:
Verifique se há intersecção entre a reta 
e o plano 
.
Solução:
Primeiramente vamos escrever as equações reduzidas da reta 
: 
. Agora vamos substituir na equação do plano:
Para calcular os valores das coordenadas 
e 
do ponto de intersecção, vamos substituir o valor de 
nas equações reduzidas da reta:
Logo, o ponto de intersecção entre a reta 
e o plano é 
.