Unidade D – O PLANO NO R³

Distâncias: distância de ponto à reta; distância de duas retas; distância de um ponto a um plano; distância de dois pontos

Quando calculamos distâncias, estamos sempre calculando a menor das distâncias. No caso de ponto à reta, traçamos um segmento da reta ao ponto, porém, esse segmento deve ser perpendicular à reta, e calculamos seu módulo. No caso de distâncias entre duas retas, esse cálculo só faz sentido se as retas forem paralelas ou reversas, já que retas concorrentes possuem distância nula no ponto de intersecção e retas coincidentes possuem distância nula em todos os pontos. No caso de distância de um ponto a um plano, traçamos um segmento do plano ao ponto, sendo este segmento perpendicular ao plano, e calculamos seu módulo. Por fim, para calcularmos a distância entre dois planos, que só faz sentido se os planos forem paralelos, traçamos um segmento perpendicular aos planos e calculamos seu módulo.

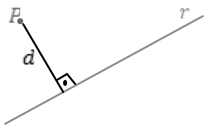
Distância de ponto à reta

Tomamos um ponto  da reta e determinamos o vetor  e com , o vetor diretor da reta, calculamos a distância de um ponto à reta da seguinte forma:

Exemplo:

Determine a distância do ponto  à reta .

Fazendo y=0 →  →

Fazendo y=1 →  →

Então    e  , portanto:

→

Distância de duas retas

1. Retas paralelas

   A distância entre duas retas paralelas, é a distância de um ponto de uma das retas até a outra reta. Como o vetor diretor das duas retas é o mesmo, temos:

   

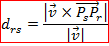
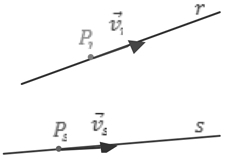
2. Retas reversas

   Para calcular a distância entre retas reversas, precisamos determinar seus vetores diretores e um vetor que vai de uma reta à outra.

   

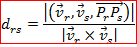
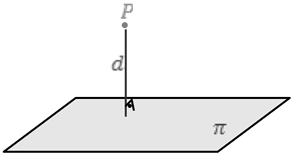
Distância de um ponto a um plano

Para calcularmos a distância de um ponto a um plano, precisamos determinar as coordenadas do vetor normal ao plano  e conhecendo as coordenadas do ponto , temos:

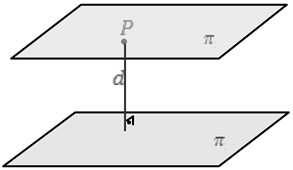
Distância de plano a plano

Para calcular a distância de um plano a outro plano, basta escolher um ponto do plano  e calcular a sua distância até o plano , ou seja, o cálculo da distância entre dois planos se resume no cálculo da distância de um ponto a um plano.

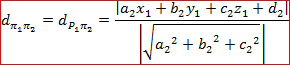
OBS.1: Se quisermos calcular a distância de uma reta a um plano, basta escolher um ponto da reta e calcular sua distância até o plano.

OBS.2: Só fazem sentido os cálculos de distâncias entre planos e entre reta e plano se os planos forem paralelos e se a reta for paralela ao plano.

Exemplos:

1) Calcule a distância entre as retas  e 

Solução:

As retas dadas são paralelas pois,  e , sendo assim:

Fazendo y=1 em  →  →

Fazendo x=0 em  →  →

Então

2) Calcule a distância entre as retas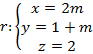      

Solução:

Vimos, na unidade anterior, que essas retas são reversas. Portanto, vamos usar a fórmula  

Como  e .

Fazendo  na reta , temos  e fazendo x=3 na reta , temos

, daí

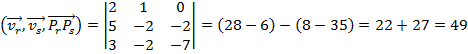
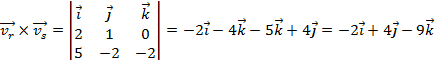
Substituindo na fórmula acima, temos

3) Calcule a distância do ponto  ao plano .

Solução:

4) Calcule a distância entre os planos  e

Solução:

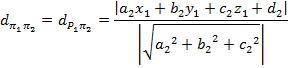
Fazendo  e sabendo que , temos: