Equação geral do plano
Que elementos são necessários para definirmos um plano? Basta uma reta? Bastam dois pontos?
Analise: Se tomarmos uma reta, podemos ter infinitos planos que a contém, basta imaginar um plano girando em torno de uma reta como se ela fosse um eixo, a cada grau, teremos um plano diferente. Se tomarmos dois pontos, teremos a mesma situação já que dois pontos distintos geram uma reta.
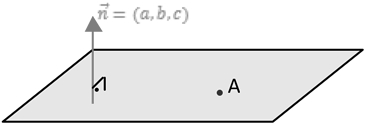
Agora vamos juntar uma reta com um ponto: se essa reta não estiver contida no plano e o ponto sim, poderemos equacionar o plano. Melhor ainda se essa reta for perpendicular ao plano. Assim definiremos um vetor, o vetor diretor da reta, ortogonal ao plano (também chamado de vetor normal ao plano) e um ponto do plano. Dessa forma, teremos um único plano que terá um vetor normal definido e um ponto que pertence ao plano.
Analise a figura D.1.
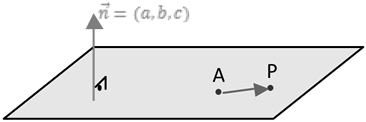
Se tomarmos um ponto 
qualquer, do plano, distinto de 
, e formarmos o vetor 
, poderemos afirmar que 
é ortogonal a 
já que 
é ortogonal ao plano, o que garante que também será ortogonal a qualquer vetor do plano ou a vetores paralelos ao plano.
Podemos então escrever a condição para vetores ortogonais: 
Desenvolvendo o produto escalar acima temos:
Como os coeficientes de 
são conhecidos e as coordenadas de 
também são, podemos substituir os termos (
) por 
e assim, a equação geral do plano fica: 
.
Exemplo:
A equação do plano 
que contém o ponto 
e possui vetor normal 
é:
Substituindo o vetor e o ponto na equação geral do plano, temos:
Para calcularmos o valor de 
, na equação do plano, podemos substituir as coordenadas do ponto 
em 
e 
da equação:
Voltando à equação do plano e substituindo o valor de 
, temos a equação geral do plano 
.
