Determinação de um plano
Vimos que para definir um plano, precisamos conhecer um ponto que pertença a ele e um vetor normal ao plano.
Outros elementos podem gerar o ponto e o vetor, são eles:
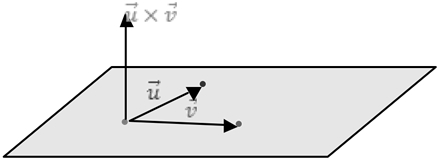
Três pontos distintos coplanares e não colineares
Com três pontos distintos, podemos formar dois vetores 
e 
distintos e com esses dois vetores, calculando o produto vetorial, geramos um vetor simultaneamente ortogonal a 
e a 
, consequentemente, ortogonal ao plano, logo: 
.
Como precisamos conhecer um ponto e nesse caso conhecemos três pontos, basta escolhermos um deles para substituirmos na equação do plano.
Exemplo:
Qual a equação do plano que contém os pontos 
, 
e 
?
Fazendo 
e 
, temos 
Escolhendo o ponto 
para substituir na equação, teremos:
Logo, 
Se tivéssemos formado outros vetores ou escolhido um dos outros dois pontos para substituir na equação, encontraríamos o mesmo plano. Pode acontecer de as equações serem múltiplas, bastando simplificá-las para verificar que geram o mesmo plano.
Verifique escolhendo outro ponto.
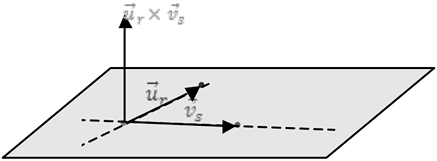
Duas retas concorrentes contidas no plano
No caso de duas retas 
e 
concorrentes, tomamos os seus vetores diretores para calcular o produto vetorial que irá gerar o vetor normal. Para encontrarmos um ponto do plano, basta tomarmos um ponto de uma das retas.
Exemplo:
Qual a equação do plano que contém as retas 
e 
Tomando os vetores diretores das retas e calculando o produto vetorial temos: 
e 
Escolhendo um ponto da reta 
, por exemplo, fazendo x=0, para substituir na equação, 
, teremos:
Logo, 
Fica como exercício determinar a equação do plano pegando um ponto da reta s.
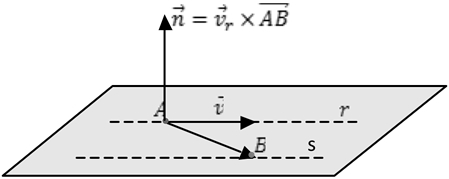
Duas retas paralelas contidas no plano
Neste caso, devemos escolher um vetor diretor e formar outro vetor com um ponto de cada reta, assim, o vetor normal será o resultado do produto vetorial entre o vetor diretor escolhido e o segundo vetor formado por um ponto de cada reta.
Exemplo:
Qual a equação geral do plano que contém as retas 
e 
?
Como as retas são paralelas, vamos escolher um ponto de cada reta para determinar o vetor 
. Sendo 
um ponto da reta 
, fazemos 
temos 
e sendo 
um ponto da reta 
, temos 
. Assim temos o vetor 
e calculando o produto vetorial entre 
e o vetor diretor da reta 
, por exemplo, temos:
Escolhendo um ponto da reta 
para substituir na equação, 
, teremos:
Logo, 
OBS.: Quaisquer outros elementos que possam determinar um plano cairão num desses casos descritos acima. Analise os elementos dados e sempre extraia um vetor normal ao plano e um ponto pertencente a ele.
Plano que passa pela origem
Se o plano passa pela origem, significa que ele contém o ponto 
, nesse caso sua equação será do tipo:
Basta substituir a origem na equação para verificar que o valor de 
se anula.