Equações paramétricas do plano
Assim como as equações paramétricas da reta, as equações paramétricas do plano são assim chamadas por possuírem parâmetros reais em suas equações.
Vimos na unidade B que podemos decompor vetores no plano e no espaço, como combinação linear de vetores dados. Pois bem, se conhecermos dois vetores não colineares de um plano, poderemos conhecer todos os outros que serão combinações lineares desses dois vetores conhecidos.
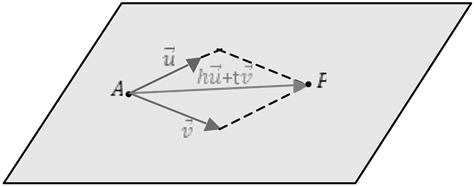
Se conhecermos um ponto ![]() e dois vetores
e dois vetores ![]() e
e ![]() não colineares, paralelos ao plano
não colineares, paralelos ao plano ![]() , poderemos escrever o vetor
, poderemos escrever o vetor ![]() (com
(com ![]() um ponto qualquer do plano) como combinação linear dos vetores
um ponto qualquer do plano) como combinação linear dos vetores ![]() e
e ![]() da seguinte forma:
da seguinte forma:
![]()
Desenvolvendo a equação acima, teremos as equações paramétricas do plano;
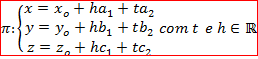
Exemplo:
As equações paramétricas do plano paralelo aos vetores ![]() e
e ![]() e que contém o ponto
e que contém o ponto ![]() são:
são:
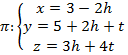 com
com ![]() e
e ![]()
![]() .
.
Se quisermos conhecer pontos do plano, basta atribuir valores para ![]() e
e ![]() .
.