Matrizes
Definição
Chama-se matriz de ordem m por n a um quadro de m´n elementos (números, polinômios, funções etc.) dispostos em m linha e n colunas, conforme a representação abaixo:
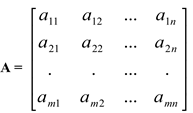
Uma forma de representação mais compacta A = [aij], em que i=1,2,3,×××,m e j=1,2,3,×××,n.
aij é o elemento genérico da matriz A.
As linhas de uma matriz são enumeradas de cima para baixo, e as colunas são enumeradas da esquerda para a direita.
Exemplo de matriz retangular de ordem 2 por 3 ou 2 X 3:
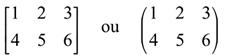
Uma matriz possui duas formas de representação, na forma de colchetes [] ou na forma de parênteses ().
Exemplo:
Represente a matriz A3x2 de acordo com o elemento genérico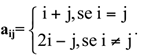 
Solução:
Calculamos cada elemento da matriz e dispomos na matriz A os valores conforme sua posição linha i e coluna j:
a11=1+1=2
a12=2×1-2=0
a21=2×2-1=3
a22=2+2=4
a31=2×3-1=5
a32=2×3-2=4
Resposta:
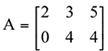
Classificação de matrizes
a) Matriz linha:
Matriz linha é uma matriz formada por uma única linha.
Ex: 
, matriz 1x3
b) Matriz coluna
Matriz coluna é a matriz formada por uma única coluna.
Ex: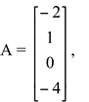 
matriz 4x1.
c) Matriz zero (nula)
Matriz zero é a matriz com todos seus elementos nulos. Uma matriz zero será denotada por 0.
Ex: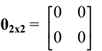 
d) Matriz quadrada
Matriz quadrada é aquela que possui o número de linhas igual ao número de colunas. Uma matriz quadrada nxn é chamada de matriz de ordem n.
Ex: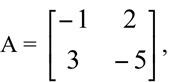 
, matriz de ordem 2.
- Diagonal principal
Numa matriz quadrada de ordem n, os elementos aij em que i=j constituem a diagonal principal.
Exemplo: No exemplo anterior os elementos -1 e -5 constituem a diagonal principal da matriz A.
- Diagonal secundária
Numa matriz quadrada de ordem n, os elementos aij em que i+j=n+1 constituem a diagonal secundária.
Exemplo: No exemplo anterior os elementos 3 e 2 constituem a diagonal secundária da matriz A.
e) Matriz diagonal
Matriz diagonal é toda matriz quadrada em que todos os elementos que não pertencem à diagonal principal são nulos.
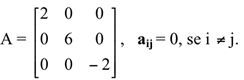
f) Matriz identidade
Matriz identidade é toda matriz diagonal em que seus elementos da diagonal principal são todos iguais a 1.
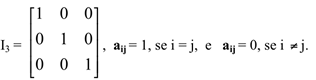
g) Matriz transposta
Matriz transposta é a matriz que se obtém transformando ordenadamente cada linha de A em coluna. Denota-se At ou A’.
Exemplos: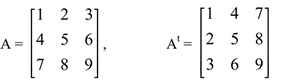 
Note que a matriz At é obtida a partir da matriz A girando (ou reflexão) em torno da diagonal principal.
Obs:
(i) (At)t = A , ou seja, a transposta da transposta de uma matriz é ela mesma.
(ii) (A ± B)t = At ± Bt
h) Matriz triangular superior
Matriz triangular superior é a matriz quadrada onde todos os elementos abaixo da diagonal principal são nulos, ou seja, aij = 0, para i>j.
i) Matriz triangular inferior
Matriz triangular inferior é a matriz quadrada onde todos os elementos acima da diagonal principal são nulos, ou seja, aij = 0, para i<j.
Exemplos:
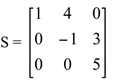é uma matriz triangular superior
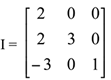é uma matriz triangular inferior
j) Matriz simétrica
Matriz simétrica é uma matriz quadrada onde aij = aji.
Obs: Neste caso, a parte superior é uma “reflexão” da parte inferior, em relação à diagonal principal
Exemplo: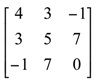
Propriedade: Uma matriz M é simétrica ↔ M = Mt
Igualdade de matrizes
Duas matrizes do mesmo tipo m x n são iguais se, e somente se, os elementos correspondentes são iguais.
Exemplo:
Se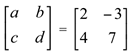
então, a =2, b = -3, c = 4, d = 7
Produto de matriz por matriz
A condição para produto entre matrizes é que o número de colunas da primeira matriz tem que ser igual ao número de linhas da segunda matriz.
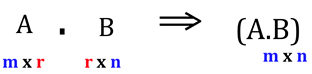
Propriedades matriciais
Supondo que os tamanhos das matrizes A, B e C são tais que as operações indicadas podem ser efetuadas e considerando a, b e c números reais, então valem as seguintes propriedades:
(a) A + B = B + A. . . . . . . . . . . . . . . . . . . . . Comutatividade da adição
(b) A + (B + C) = (A + B) + C . . . . . . . . . . . . Associatividade da adição
(c) A(BC) = (AB)C . . . . . . . . . . . . . . . . . . . . Associatividade da multiplicação
(d) A(B ± C) = AB ± AC . . . . . . . . . . . . . . . . Distributividade à esquerda
(e) (A ± B)C = AC ± BC . . . . . . . . . . . . . . . . Distributividade à direita
(f) a(B ± C) = aB ± aC . . . . . . . . . . . . . . . . Distributiva da multiplicação em relação à adição de matrizes
(g) (a ± b)C = aC± b . . . . . . . . . . . . . . . . . Distributiva da adição de escalares em relação à multiplicação
(h) a(bC) = a(bC) . . . . . . . . . . . . . . . . . . . . Associativa
(i) a(BC) = (aB)C = B(aC) . . . . . . . . . . . . . . . Associativa
Cuidado! Em geral AB ≠ BA
Exemplo:
Sejam as matrizes: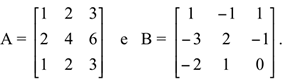 
(a) Calcule AB e BA.
(b) Determine (B×A)t e At×Bt. Comparar os resultados.
Solução:
a)
Note que:
i) B×A=0, mas B≠0 e A≠0.
ii) A×B ≠ B×A
b)
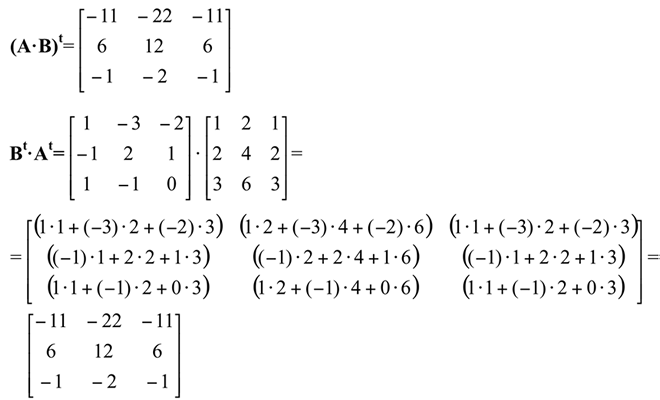
Comparando os resultados, obtemos a conclusão em que (A×B)t = Bt×At, isso é devido à propriedade “j” descrita abaixo.
Outras propriedades:
(j) (AB)t = BtAt
(k) AI = IA = A
(l) A.0 = 0.A = 0
Matriz inversa
Uma matriz quadrada A de ordem n é inversível se, e somente se, existir uma matriz B tal que AB = BA = In, onde In é a matriz identidade de ordem n.
No caso da matriz B existir, utiliza-se a seguinte notação: B = A-1 (lê-se B é igual à inversa de A).
Exemplo:
Verifique se as matrizes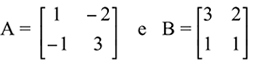 
são matrizes inversas uma da outra.
Solução:
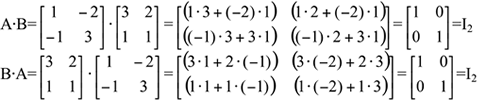
Ou seja, A×B= B×A=I2
Importante:
Nem sempre uma matriz é inversível.
Uma matriz A é inversível se, e somente se, o determinante de A for diferente de zero(detA≠0). Veremos a definição e como calcular determinantes logo em seguida.
Propriedades da matriz inversa
Sejam A e B matrizes inversíveis. Então valem as propriedades:
(i) (A-1)-1 = A
(ii) (AB)-1 = B-1A-1
(iii) (At)-1 = (A-1)t A inversa da transposta é a transposta da inversa
Exemplo:
Determine a matriz inversa da matriz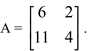 
Esta matriz tem inversa pois det A ≠0. Procuremos sua inversa tal que A.B = I e B.A = I.
Supondo que 
, basta determinar o valor de a, b, c, e d. Impondo a primeira condição temos,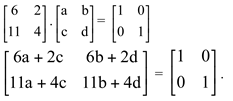
Portanto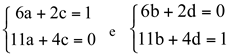
Resolvendo os sistemas, temos
a = 2, b = -1, c = -11/ 2, d = 3
Portanto,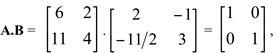 
ou seja, A.B = I2. Também vale B.A = I2.
Desta forma concluímos que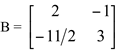 
é a matriz inversa de A.