Determinantes: definição; cálculo de segunda, terceira e qualquer ordem de determinantes; propriedades
O conceito de determinante de uma matriz quadrada surge a partir de somas e produtos de permutações dos elementos da matriz. Aqui, vamos tratar esse assunto de uma forma direta aos cálculos de determinantes. Determinante é um número associado a uma matriz quadrada. Esse número caracteriza várias situações como, por exemplo, se uma matriz é inversível, as características de um sistema e no caso da matriz representar uma transformação, caracteriza se transformação está amplificando ou atenuando o elemento que está sendo transformado.
Determinantes de 2a ordem
Dada a matriz 
, então o determinante de A, denotado por 
.
Exemplo:
Determinantes de 3a ordem
Dada a matriz 
, então pela regra de Sarrus
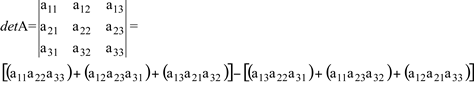
Exemplo:
Calcule o determinante da matriz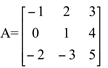 
Solução:
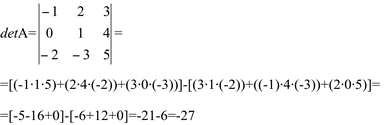
Portanto: detA==-27
O teorema de Laplace
Cofator:
Dada a matriz A=[aij], de ordem n, então o cofator será Cij = (-1)ijDij, em que Dij é o determinante da matriz A retirando a i-ésima linha e a j-ésima coluna.
Considere a matriz A=[aij] de ordem 3, o cálculo do determinante usando a 1a linha é dada por:
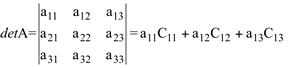
Exemplo:
Calcule o determinante da matriz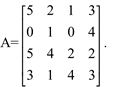 
Obs.:
1) Para calcular determinantes de matrizes com ordem maior do que 3 uma alternativa é usar o teorema de Laplace.
2) Como, para este exemplo, a linha ou coluna que se apresenta com maior números de zeros é a linha 2, então, a melhor escolha para usar o teorema de Laplace é a linha 2.
Solução:
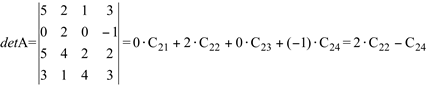
Então, necessitamos calcular os cofatores C22 e C24
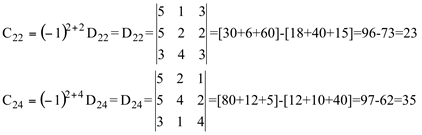
Portanto, detA= 2 x C22 - C 24 = 2 × 23 - 35 = 46 - 35 = 11
Propriedades dos determinantes:
a) O determinante de uma matriz A não se altera quando se troca as linhas pelas colunas, ou seja detA = detAt.
Exemplo:
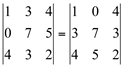
b) Se a matriz A possui uma linha (ou coluna) constituída de elementos todos nulos, o determinante é nulo.
Exemplo:
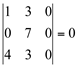
c) Se a matriz A tem duas linhas (ou duas colunas) iguais, o determinante é nulo.
Exemplo:
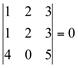Obs.: Os elementos da 1a linha e da 2a linha são iguais.
d) Se na matriz A duas linhas (ou duas colunas) têm seus elementos correspondentes proporcionais, o determinante é nulo (numa matriz A, dois elementos são correspondentes quando, situados em linhas diferentes, estão na mesma coluna, ou quando, situados em colunas diferentes, estão na mesma linha).
Exemplo:
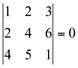Obs.: A 2a linha é o dobro da 1a linha.
e) Se na matriz A cada elemento de uma linha (ou coluna) é uma soma de duas parcelas, o determinante de A pode ser expresso sob a forma de uma soma dos determinantes de duas matrizes, isto é:
Exemplo:
f) O determinante de uma matriz diagonal A (superior ou inferior) é igual ao produto dos elementos da diagonal principal:
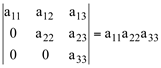
Exemplo:
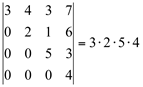
g) Trocando-se entre si duas linhas (ou colunas) da matriz A, o determinante muda de sinal, isto é, fica multiplicado por (-1).
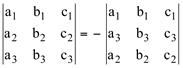
Exemplo:
Calcular
1) 
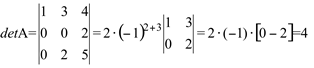(usando o teorema de Laplace)
2) 
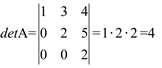(usando o teorema de Laplace)
h) Quando se multiplicam por um número real todos os elementos de uma linha (ou de uma coluna) da matriz A, o determinante fica multiplicado por esse número:
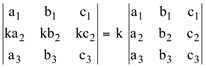
Exemplo:
Calcular
1) 
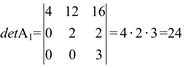
2) 
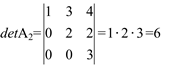
Portanto: detA1 = 4 × detA2
Obs.: A 1a linha da matriz A1 é igual a 4 vezes a 1a linha da matriz A2.
i) Um determinante não se altera quando se somam aos elementos de uma linha (ou uma coluna) da matriz A os elementos correspondentes de outra linha (ou coluna) previamente multiplicados por um número real diferente de zero:
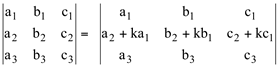
Exemplo: (L'2=L2+3L1)
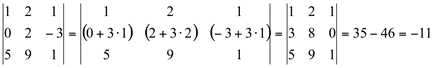
Operações elementares:
1) L'3 = L3-5×L1
2) L'3=2×L3
3) L'3=L3+L2