Sistemas de equações lineares
Equações lineares
Equação linear é uma equação da forma a1x1+a2x2+a3x3+...+anxn=b, na qual, x1,x2,x3,...,xn são as variáveis, a1,a2,a3,...,an são os respectivos coeficientes das variáveis e b é o termo independente.
Os valores (raízes) das variáveis que verificam a equação constituem o conjunto de soluções.
Existem três possibilidades de soluções.
Vamos analisar três situações bem simples.
Pergunta-se: Qual é o valor de “x”?
1) 0.x=6 → Solução impossível (não tem solução).
2) 2.x=6 → Solução possível e determinada (uma única solução).
3) 0.x=0 → Solução possível e indeterminada (infinitas soluções).
Sistema de equações lineares (SEL)
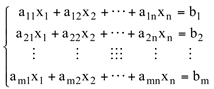
Forma matricial: A.X=B em que
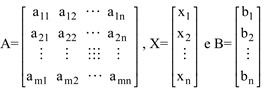
A solução de um SEL é a n-upla Xt=[x1,x2,...,xn] que verifique, simultaneamente, todas as equações do sistema linear.
Classificação do SEL
Sistema possível ou compatível é o SEL que admite solução.
Sistema impossível ou incompatível é o SEL que não admite solução.
O sistema possível se divide em outras duas classes:
Sistema possível e determinado é o SEL que admite uma única solução.
Sistema possível e indeterminado é o SEL que admite mais de uma solução (na verdade, admite infinitas soluções).
Exemplos:
Resolver e classificar os sistemas:
a)![]()
Substituindo o valor de y na 1ª equação: 2x+3.4=18 → x=3
Portanto, a solução é S={(3,4)} e a classificação é compatível (ou possível) e determinado (uma única solução).
b) ![]()
As duas equações, na verdade, são iguais. Então a solução é dada apenas por uma, ou seja, 4x+2y=100 → y=50-2x.
Portanto, a solução é dada por S={(x,y)/y=50-2x} e a classificação é compatível(ou possível) e indeterminado(uma infinidade de soluções).
c)![]()
Concluímos que não existe x tal que 0.x=3.
Portanto. a solução é dada por S={} e a classificação é incompatível (ou impossível) (não tem solução).
Sistemas equivalentes
Dois sistemas de equações lineares são equivalentes quando admitem a mesma solução.
As operações elementares efetuadas nas matrizes também podem ser usadas em sistemas de equações lineares. Dois sistemas de equações lineares são equivalentes se diferem por uma operação elementar.
Sistema linear homogêneo
Quando em um sistema de equações lineares os termos independentes são todos nulos, o sistema é chamado homogêneo.
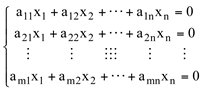
ou na forma matricial A.X=0, em que B=0(vetor nulo).
Todo sistema homogêneo admite a solução X=0, denominada, solução trivial, em que xi=0 representam as variáveis para i=1,2,...,n.
Estudo e solução dos sistemas de equações lineares
Método da matriz inversa
Dado um sistema de equações lineares na forma matricial A.X=B. Multiplicando a equação matricial por A-1 pela esquerda, temos:
A-1.A.X=A-1.B
I.X=A-1.B
X=A-1.B
Este método resolve apenas sistemas com n equações e n variáveis.
Exemplo:
Resolva o sistema![]() .
.
Solução:
Escrevendo na forma matricial ![]() , em que
, em que ![]() e
e ![]() .
.
Vamos calcular a matriz inversa da matriz A
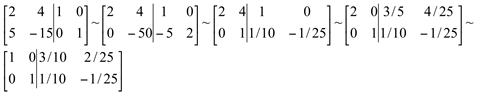
Operações elementares:
1) L'2=2.L2-5.L1
2) L'2=L3/(-50)
3) L'1=L1-4.L2
3) L'1=L1/2
Então a matriz inversa da matriz A é 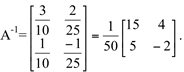
Portanto:
![]()
Solução: S={(5,3)}
Note que para a matriz ![]() temos
temos ![]() , em que detA=-50.
, em que detA=-50.
Para uma matriz genérica de segunda ordem ![]() , temos uma relação geral para matrizes de segunda ordem
, temos uma relação geral para matrizes de segunda ordem ![]() .
.
Método de Gauss-Jordam
Redução de um sistema de m equações lineares em n incógnitas usando a forma escalonada:
- Passo 1: Permutar as equações de maneira que a primeira incógnita x1 apareça com coeficiente diferente de zero na primeira equação, ou seja, faça com que
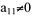 .
. - Passo 2: Usar a11 como pivô para eliminar x1 de todas as outras equações, exceto a primeira. Isto é, para cada i>1, aplique a operação elementar:
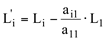 .
. - Passo 3: Examine cada nova equação L:
(a) Se a equação L tem a forma 0.x1+0.x2+.+0.xn=0, ou se a equação L é múltipla de outra equação, retire a equação L do sistema.
(b) Se a equação L tem a forma 0.x1+0.x2+.+0.xn=b, com b≠0, o sistema não tem solução. - Passo 4: Repita os passos 1, 2 e 3 com o sistema formado por todas as equações menos a primeira.
- Passo 5: Continue o processo até que o sistema esteja na forma escalonada ou que apareça uma equação degenerada tal como em (b) do passo 3.
Exemplos:
Resolver e classificar os sistemas:
1)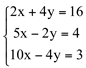
Solução:
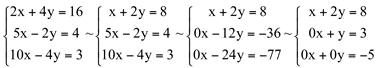
Operações elementares:
(1) L'1=L1/2
(2) L'2=L2-5×L2 L'3=L3-10×L1
(3) L'2=L2/(-12) L'3=L3-2×L2
Como 0.x+0.y=-5, então não existe x e y tal que 0.x=-5 ou 0.y=-5.
Portanto: S={} e o sistema é impossível.
2)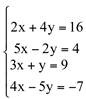
Solução:
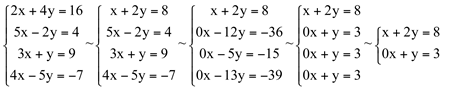
(1) L'1=L1/2
(2) L'2=L2-5.L2 L'3=L3-3.L1 L'4=L4-4.L1
(3) L'2=L2/(-12) L'3=L3/(-5) L'4=L4/(-13)
Como temos 0.x+y=3, então y=3 e como x=8-2y ou x=8-2.3=2.
Portanto, o conjunto solução é S={(2,3)} e o sistema é possível e determinado.
3)![]()
Solução:
![]()
Operações elementares:
(1) L'1=L1/2 L'2=L2/2
(2) L'2=L2-2×L2
Como 0x+y+2z+3w=11, então y=11-2z-3w e x=42+4y-12z-9w ou x=42+4.(11-2z-3w)-12z-9w=42+44-8z-12w-12z-9w=86-20z-21w.
Portanto: ![]() e o sistema é possível e indeterminado.
e o sistema é possível e indeterminado.