Unidade F – Espaços Vetoriais

Definição

Seja V um conjunto não vazio, sobre o qual estão definidas as operações de adição e de multiplicação por escalar, isto é,

 A, B  V temos:  A + B  V  e,

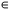
A  V   e      temos:   A V,

onde V com essas operações é chamado de espaço vetorial real se forem verificados os 8 axiomas:

Sejam A, B, C  V   e ,  

(A₁)  (A + B) + C = A + (B + C)

(A₂)  A + B = B + A

(A₃)  um único elemento neutro O V  tal que A + O = O + A = A

(A₄)  um único elemento simétrico  -A  V  tal que  A + (-A) = O

(M₁)    (.)A  =(A)

(M₂)    (+)A = A +A

(M₃)  (A + B) = A +B

(M₄)   1A = A

Obs:

Os elementos de um espaço vetorial V podem ser polinômios, matrizes, números, funções, desde que as operações definidas neste conjunto satisfaçam os 8 Axiomas.

Mas, independente de sua natureza, os elementos de um Espaço Vetorial V serão chamados de vetores.