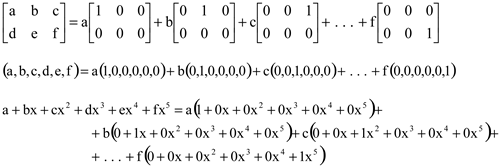Propriedades e exemplos de espaços vetoriais
Vamos, agora, discutir sobre alguns exemplos de conjuntos com as operações de adição e multiplicação por escala se é ou não é um espaço vetorial.
Obs.:
(1) Qualquer dúvida na validade de alguma propriedade vista ou não, o aluno deve verificar a propriedade, sempre, tomando como elementos genéricos dos conjuntos. A verificação de um exemplo específico não quer dizer que a propriedade vale para outro exemplo, ou seja, um exemplo não prova nada. Então, para fazer uma prova, temos que tomar, sempre, elementos genéricos dos conjuntos para verificar as propriedades.
(2) Ficam como exercícios os axiomas que não verificamos.
Exemplo a:
V = M(2x2) = 
(Conjunto das matrizes 2x2).
Em V é definido as operações:
Sejam A, B 
V onde 
, 
e 
- Adição → A + B =
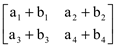
- Multiplicação por escalar → 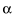A=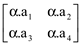
Obs: Essas são as operações usuais de adição e multiplicação por escalar no conjunto das matrizes 2x2.
Para essas operações assim definidas, podem ser verificadas facilmente que valem os 8 axiomas.
Portanto, neste exemplo, V = M(2x2) é um espaço vetorial.
Exemplo b:
V = 
(Conjunto das matrizes linha M(1x3))
Operações definidas:
(Cuidado, adição não usual)
(Multiplicação usual)
Com estas operações, V é um espaço vetorial?
Verificando os axiomas:
Sejam A = 
, B = 
, C = 
A1) (A + B) + C = A + (B + C) ?
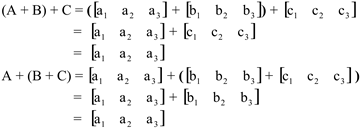
O Axioma A1 é satisfeito.
A2) A + B = B + A ?
Como o axioma A2 falha, V não é um espaço vetorial.
| ||||
| ||||
|
Exemplo c:
V ={(x,y)Î 
} (Conjunto dos vetores em )
Operações definidas, (a, b) + (c, d) = (a +c, b + d) e (a,b)= (2a,2b)
Como a adição é uma operação usual, vamos verificar se falha algum axioma em relação à multiplicação por escalar.
Sejam u = (a, b) e v = (c, d) em , e 
números reais.
M1) (.)u = (u) ?
(.)u = (.)(a, b) = (²² a, ²²b)
(u) = ((a,b)) = (² a, ² b) = (²²a, ²²b), logo (.)u = (u) e o axioma M1 é satisfeito.
M2) (+)u = u +u ?
(+)u = (+)(a,b) = ((+)2.a, (+)2.b)
u +u = (a,b) +(a,b) = (²a,²b) + (²a, ²b) = ((²+²)a, (²+²).b)
O axioma M2 não é satisfeito pois (+)u ≠u +u 
.
Como 
, então V ={(x,y) ∈ 
} com as operações definidas, não é um espaço vetorial.
Exemplo d:
V = M(m,n) (Conjunto das matrizes mxn) com as operações usuais (de adição e de multiplicação por escalar) definem um espaço vetorial.
Obs: Se A ∈ M(mxn), então A =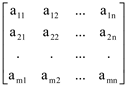 
Exemplo e:
V = 
= {(x1, x2, x3, ... , xn): xi ∈
}, em que 1 ≤ i ≤ n, com as operações de adição e de multiplicação por escalar usuais definem um espaço vetorial.
Exemplo f:
V = P3 (Conjunto dos polinômios com coeficientes reais de grau menor ou igual a 3) (incluindo os polinômios de grau zero)
ou P3 = { a0 + a1x + a2x2 + a3x3: ai ∈ }
Exemplos de elementos de P3:
3, 2 + 5x, 3x², 1 - 5x³, -3 + 6x – 4x² + 7x³
Se p1(x) e p2(x) pertencem a P3 então:
p1(x) = a0 + a1x + a2x² + a3x³ e p2(x) = b0 + b1x + b2x² + b3x³
Operações usuais em P3:
p1(x) + p2(x) = (a0 + b0)+ (a1 + b1)x + (a2 + b2)x² + (a3 + b3)x³
Se ∈ temos.p1(x) =a0 +a1x + a2x² + a3x³
Com estas operações pode-se verificar que V =P3 é um espaço vetorial.
Exemplo g:
O conjunto 
das funções reais definidas em toda a reta.
Se f,g ∈V e 
, tem-se: 
e 
O conjunto V com essas operações é um espaço vetorial.
Observações:
Matrizes, vetores, polinômios podem estar associados uns aos outros.
Por exemplo,
A = 
v = (a, b, c, d, e, f)
p(x) = a + bx + cx2 + dx3 + ex4 + fx5
A ∈ M(2,3), v ∈ 6 , p(x) ∈ P5
Diz-se que a, b, c, d, e, f são as coordenadas de A, v e p(x). Por isso, matrizes, vetores, polinômios são chamados de maneira geral vetores, independentemente de sua natureza. A justificativa está no fato de as operações de adição e multiplicação por escalar realizadas com elementos de natureza tão distinta se comportarem de forma idêntica, como se estivessem trabalhando com os próprios vetores do 6, da seguinte forma:
