Unidade F – Espaços Vetoriais

Subespaços vetoriais

Deseja-se dentro de um espaço vetorial V, detectar se um subconjunto S de V é também espaço vetorial. Tais conjuntos serão chamados subespaços de V.

Exemplo:

V = ²  com as operações usuais de adição e multiplicação por escalar é um espaço vetorial.

S é um conjunto de vetores que pertencem a uma reta que passa pela origem. Neste caso, S é um subconjunto de V.

S ⊂ V =
S = {(x,y) : x = 3y} =

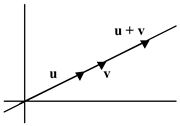
Observa-se que ao somarmos 2 vetores de S, obtemos outro vetor em S. E se multiplicarmos um vetor de S por um número, o vetor resultante estará em S.

u = (3,1),   v = (9, 3),

u + v = (12, 4)

Definição:

Seja V um espaço vetorial e S um subconjunto não vazio de V.

S é um subespaço vetorial de V se:

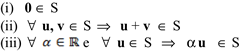
Propriedades

Qualquer subespaço S de V deve conter o vetor nulo 0 (devido ao Axioma A3 do Espaço Vetorial). Caso contrário S não é um subespaço vetorial.

Todo espaço vetorial  admite pelo menos 2 subespaços (chamados subespaços triviais), o conjunto {0} (subconjunto formado somente pelo elemento zero) e o próprio espaço vetorial V.

Exemplos de subespaços vetoriais

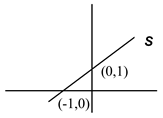
(a)  Seja V =  com as operações usuais o espaço vetorial  S = .

S  pode ser representada por um conjunto de vetores pertencentes a uma reta que passa pelos pontos (-1,0) e (0,1).

O vetor nulo   ( 0,0 )  S   S não é um subespaço vetorial de V.


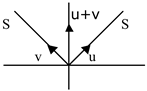
(b)  Seja  V =  com as operações usuais o espaço vetorial e .

S não é vazio, pois .

Mas, existem 2 vetores  u  e  v  de S  tais que  (u + v)  S.

Por exemplo, u = (1,1), v = (-1,1) pertencem a S  e  u + v = (0,2)  S.

Portanto, S não é um subespaço de V = .

(c) Seja V =  com as operações usuais o espaço vetorial e S = .

Obs:  S é um conjunto de vetores pertencentes a um plano que passa pela origem.

S é um subespaço de V ?

Solução:

Vamos verificar se em S satisfazem as condições (I), (II) e (III).

(I) (0,0,0)  S,   pois  a0 + b0 + c0 = 0.

(II) Sejam  u = (u1, u2, u3), v = (v1, v2, v3) elementos de S.

Então,      u+v = (u1+v1 , u2+v2 , u3+v3).

Logo, a(u1+v1) + b(u2+v2) + c(u3+v3) = (au1+bu2+cu3) + (av1+bv2+cv3) = 0+0 = 0. Portanto, (u1 + v1, u2 + v2, u3 + v3) S.

Daí,  u + v S.

(III) Seja   e  u = (u1, u2, u3) .

Se u  S, então  au1 + bu2 + cu3 = 0    e     u = (u1 + u2 + u3).

Portanto,   au1 + bu2 + cu3 = ( au1 + bu2 + cu3) = 0 = 0. Dai u  S.

Como as 3 condições foram satisfeitas, S é um subespaço de V = .

Intersecção e Soma de Subespaços

Teorema:

Sejam S1 e S2  subespaços vetorias de V (espaço vetorial).

Então,

(i)   S1 ∩ S2  é um subespaço de V.

(ii)  S1 + S2  é um subespaço de V.

OBS:

S1 ∩ S2  = {v V:  v S1   e  v  S2}

S1 + S2  =   { v = u + w /  u S1   e   w S2}.

Todo elemento de S1 + S2  é um vetor soma de 2 vetores, um vetor de S1 e o outro de S2.

Exemplos:

a) seja V = M(3 x 3) o espaço vetorial das matrizes de ordem 3 e

S1 = 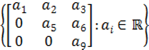        e        S2 =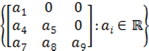

S1  e  S2 são subespaços de V = M(3 x 3)
S1 = {matrizes triangulares superiores}
S2 = {matrizes triangulares inferiores}

Logo, S1 ∩ S2  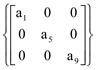=   é um subespaço de V = M(3 x 3)


b) Seja V =  o espaço vetorial,

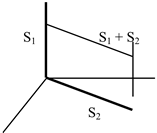
S1 = {(0, 0, x):  x }  é um conjunto de vetores pertencentes a reta no eixo z  e  S2 = {(a, a, 0):  a  }  é um conjunto de vetores pertencentes a uma reta no plano xy.

S1 + S2 = {(a,a,x)} é o conjunto de vetores pertencentes ao plano que contém as retas na qual os vetores de S1 e S2 pertencem.

S1 + S2 é um subespaço de V = .

Soma Direta de Subespaços

Definição:

Sejam S1 e S2 subespaços vetoriais de V. Então V é a  soma direta  de S1 e S2 (Representado por V = S1  S2 ), se  V = S1 + S2   e   S1 ∩ S2 = { 0 }.

Seja o espaço vetorial das matrizes de ordem 2 V = M(2 x 2). Sejam os subespaços vetorais S1=   e S2=   onde  a, b, c, d . Então, S1 + S2 =  = M(2 x 2)  e  S1∩ S2  = .

Logo, V = S1  S2   e  portanto V é soma direta de S1 e S2.