Subespaço finitamente gerado
Definição
Sejam v1, v2, ... , vn
V (espaço vetorial). O conjunto de todos os vetores que são combinação linear de v1, v2, ... , vn é um subespaço vetorial de V. Este conjunto é representado por
S = [v1, v2, ... , vn] = {v V / v = a1v1 + a2v2 + ... + anvn}
S é denominado subespaço gerado por v1, v2, ... , vn.
Obs: Seja A = {v1,v2, ... ,vn} o conjunto gerador de S.
G(A) é o subespaço gerado por A, isto é, G(A) = [v1,v2, ... ,vn] = S.
Exemplos:
1)Seja V = 
e u = (3,4,5) 
.
Determine o subespaço gerado por u, isto é, encontrar S = [u] .
Solução:
S = [u] = {(x,y,z) / (x,y,z) = a(3,4,5), em que a 
}.
Daí, x =3a, y = 4a, z = 5a
De x =3a temos a = 
, substituindo a em y e z ficamos com,
y = 
e z = 
.
Resposta: S = [u] = {(x, , )} / x }. (Conjunto de vetores pertencentes a uma reta que passa na origem)
Obs: Se u é um vetor não-nulo de , S = [u] é um conjunto de vetores pertencentes a uma reta que passa pela origem.
2) Seja V = , encontre S = [v1, v2], em que v1 = (2,0,1) e v2 = (0,3,3).
Solução:
[v1, v2] = {(x,y,z) / (x,y,z) = a1(2,0,1) + a2(0,3,3)}. Logo temos,
(x,y,z) = (2a1, 0, a1) + (0, 3a2, 3a2) = (2a1, 3a2, a1 + 3a2)
Portanto, 2a1 = x, 3a2 = y e a1 + 3a2 = z
(x,y,z) [v1, v2] 
o sistema anterior tem solução.
Substituindo a1= x/2 e a2= y/3 na 3a equação a1 + 3a2 = z obtém-se,
ou x + 2y - 2z = 0 (plano que contém v1 e v2 e passa na origem)
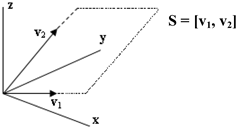
Portanto, (x,y,z) pode ser escrito como combinação linear de v1 e v2, se e somente se, (x,y,z) satisfaz a equação x + 2y - 2z = 0.
Resposta: [ v1, v2] = {(x,y,z) / x + 2y - 2z = 0 } (Conjunto de vetores pertencentes ao plano que contém v1e v1)
3) Seja V = 
, determine S = [u1, u2], em que u1= (1,0),u2 = (0,1).
Solução:
[u1, u2] = {(x,y) / (x,y) = a1(1,0) + a2(0,1)}.
(x,y) = a1(1,0) + a2(0,1) 
(x,y) = (a2,a2), ou seja, qualquer vetor (x,y) pode ser escrito como combinação linear de (1,0) e (0,1), bastando que a2 = x e a2 = y, ou seja, não têm restrições.
Portanto, [u1, u2] = {(x,y) } =
4) Seja V = , encontrar S = [v1, v2, v3], em que v1 = (1,0,0), v2 = (0,1,0), v3 = (0,0,1).
Solução:
[v1, v2, v3] = {(x,y,z) / (x,y,z) = a1(1,0,0) + a2(0,1,0) + a3(0, 0,1)}. Logo temos,
(x,y,z) = (a1, 0, 0) + (0, a2, 0) + (0, 0, a3) = (a1, a2, a3)
Então, qualquer vetor (x,y,z) pode ser escrito como combinação linear de (1,0,0), (0,1,0), (0, 0,1), já que a1 = x, a2 = y, a3 = z.
Portanto, [v1, v2, v3] =
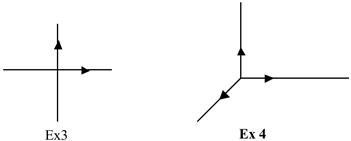
Observe nos gráficos das figuras que os vetores de são não paralelos e os vetores de são não coplanares.
Conclusões:
Dos exemplos 3 e 4, podemos obter algumas generalizações:
Sejam u1, u2 (Plano) e v1, v2, v3 (Espaço) (todos não nulos)
(i) Seu1, u2 são não paralelos, então [u1, u2] =
(ii) Se v1, v2, v3 são não coplanares, então [v1, v2, v3] =