Dependência e Independência Linear
Seja v3 um vetor pertencente ao mesmo subespaço gerado por v1 e v2 então o subespaço gerado por v1 e v2 é o mesmo subespaço gerado por v1, v2 e v3, isto é,
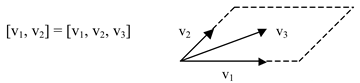
A razão disso é que v3é um vetor a mais para descrever o subespaço, pois v3 é uma combinação linear de v1 e v2.
Em nosso estudo, estamos interessados em determinar dentre um conjunto de n vetores {v1, v2, ... , vn}, o “menor” conjunto gerador de um subespaço, denominado Base. Para isso, precisamos definir dependência e independência linear.
Definição
Sejam v1, v2, ... , vn 
V (espaço vetorial).
O conjunto {v1, v2, ... , vn} é linearmente independente (LI), se a equação
a1v1 + a2v2 + ... + anvn = 0 ← Vetor nulo
admitir apenas a solução trivial (a1 = a2 = ... = an = 0 )
Caso exista algum ai ≠ 0, então o conjunto {v1, v2, ... , vn} é dito linearmente dependente (LD).
Exemplos:
(1) Seja V = 
e v1, v2,v3 V tal que v1 = (1,0) e v2 = (0,1). O conjunto { v1, v2 } é LI ou LD ?
Solução:
Este conjunto é LI pois da equação a1v1 + a2v2 = (0,0) temos,
a1(1,0) + a2(0,1) = (0,0) 
a1 = a2 = 0.
(2) Seja V = 
e v1,v2,v3 V tal que v1 = (1,1,2), v2= (3,-8,-5) e v3= (-2,8,6).
O conjunto {v1, v2,v3} é LI ou LD ?
Solução:
Da equação a1v1 + a2v2 + a3v3 = (0,0,0) temos,
a1(1,1,2) + a1 (3,-8,-5) + a3(-2,8,6) = (0,0,0)
Daí tem-se o seguinte sistema homogêneo,
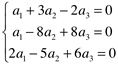
Sabe-se que todo sistema homogêneo admite a solução trivial. Portanto, verificaremos se o sistema admite outra solução, caso exista, o conjunto {v1, v2,v3} é LD.
Escrevendo o sistema na forma de uma matriz ampliada e em seguida utilizando o processo de escalonamento, temos:
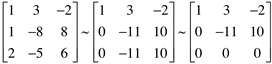
Operações:
1) L’2 =L2 – L1
2) L’3= L3 – L2
3) L’3= L3 – L1
Portanto, -11a2 + 10a3 = 0 e a1 + 3a2 - 2a3 = 0 (Sist. Indeterminado)
Então 
e 
Logo, para qualquer a3 ≠ 0, temos uma solução não trivial. Por exemplo, se a3 = 11, temos a2 = 10 e a1 = -8, ou seja, -8(1,1,2) + 10(3,-8,-5) + 11(-2,8,6) = (0,0,0).
Então, o conjunto {v1, v2,v3} é LD.
Obs: Para escalonar sistemas homogêneos não há necessidade de incluir a coluna das constantes formada por zeros.
Outra forma de resolver o sistema é usando a regra de Cramer:
Calculando o determinante da matriz principal
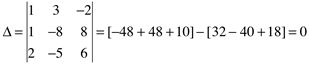
Como 
, 
e 
, pois uma coluna é toda de zeros devido aos termos independentes, e pela regra de Cramer, temos: 
, 
e 
. Portanto 
, 
e ou 
, 
e 
.
Logo, existe uma solução que não é a trivial, daí o conjunto {v1, v2,v3} é LD.
Obs.:
(i)
Se 
, então o conjunto de vetores é LD.
(ii) Se 
, então o conjunto de vetores é LI.
Teorema:
O conjunto {v1, v2, ... , vn} é LD 
Se um dos vetores vi (i=1,2,...,n) for combinação linear dos outros.
Exemplos:
(1) No conjunto {v1, v2,v3}, em que v1 = (2,1,3), v2 = (10,5,15), v3 = (4,5,9), nota-se que:
v2= 5v1+ 0v3, isto é, v2é uma combinação linear de v1 e v3.
Logo, o conjunto {v1, v2,v3} é LD.
(2) Seja {v1, v2, v3}, em que v1 = (2,4,5), v2 = (8,1,12). v3 = (10,5,17)
Observe que: v3 = v1 + v2. Então o conjunto {v1, v2, v3} é LD.
OBS: Uma outra versão do teorema é:
O conjunto {v1, v2, ... , vn} é LI
Nenhum destes vetores foi combinação linear dos outros.