Base de um Espaço Vetorial
Pergunta-se: “Quantos vetores têm o espaço vetorial 
?”
Uma infinidade. Imagina se temos que efetuar operações ou verificar propriedades desse espaço vetorial, tendo que trabalhar com um número infinito de vetores?
Agora, por outro lado, como dois vetores LI geram o espaço , então, basta termos dois vetores LI que geram o para podermos, simplesmente, trabalhar com esses dois vetores na qual representam todos os vetores do .
Portanto, desejamos encontrar um número finito de vetores de um espaço vetorial V que sejam necessários para gerar V. Um conjunto deste tipo denomina-se Base de V.
Definição
Seja o conjunto B = {v1, v2, ... , vn} 
V (espaço vetorial).
B é uma base de V se:
(I) o conjunto B é LI;
(II) o conjunto B gera V, isto é, [v1, v2, ... , vn] = V
Exemplos:
1) O conjunto B = {(1,1), (0,1)} é base de V = ?
Basta verificar se B é LI e se B gera .
(I) a1(1,1) + a2(0,1)=(0,0) 
a1 = 0 e a1 + a2 = 0 a1 = a2 = 0.
Logo, B é LI.
(II) B gera se para qualquer v=(x,y) 
pode ser escrito como combinação linear de (1,1) e (0,1).
De (x,y) =a1(1,1) + a2(0,1) temos, a1 = x e a1 + a2 = y
Daí, a2 = y - a1 = y – x.
Portanto, (x,y) = x(1,1) + (y-x)(0,1). Então, B gera .
Como foram satisfeitas as condições (I) e (II), o conjunto B é uma base de .
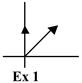
(2) Seja F = {(0,1), (0,2)} não é base de pois F é um conj. LD, já que (0,2) = 2(0,1), ou seja, (0,2) é uma combinação linear de (0,1).
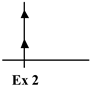
(3) Seja V = e e1 = (1,0) e e2 = (0,1).
O conjunto {e1, e2} é denominado base canônica de .
(4) Seja V = 
e e1 = (1,0,0), e2 = (0,1,0) e e3 = (0,0,1).
O conjunto {e1, e2, e3} é denominado base canônica de .
Teorema: Qualquer base de um espaço vetorial V tem sempre o mesmo número de elementos.
Este número é denominado dimensão de V, cuja notação é dim V.
Exemplos:
(1) Seja o espaço vetorial V = . Os conjuntos B1 = {(1,0), (0,1)} e B2 = {(1,1), (0,1)} são bases de V = , então dim = 2.
(2) Seja V = (espaço vetorial), então dim = 3.
(3) V = 
(espaço vetorial), então dim = n.
(4) Seja V = M(2,2) (espaço vetorial), então dim M(2,2) = 4.
O conjunto 
forma uma base (base canônica) de M(2,2).
Corolário (Consequência do Teorema)
Se dim V = n então:
(a) qualquer conjunto com mais de n vetores é LD.
(b) qualquer conjunto de n vetores LI é uma base de V.
Exemplos:
(1) Seja o conjunto C = {(1,0,0), (0,1,0), (3,4,7),(5,8,6)}.
Como dim = 3 e o conjunto possui 4 vetores, então o conjunto C é LD. (Pelo corolário (a)).
(2) Seja D = {(1,2,3), (-1,1,-1), (2,-1,4)}, então o conjunto D é base de ?
Como dim = 3 e D possui 3 vetores.
Então, se o conjunto D for LI, pelo corolário (b), D será uma base de .
Verificando se D é LI.
De x(1,2,3) + y(-1,1,-1) + z(2,-1,4) = (0,0,0) temos,
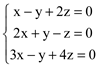Resolvendo este sistema por escalonamento temos, x = y = z = 0.
Portanto, o conjunto D é LI e forma uma base de .
(3) Determinar a dimensão e uma base para cada um dos seguintes subespaços vetoriais:
(a) V = , A = {(x,y,z)/ z = 4x}
Solução:
A = {(x,y, 4x)}. Nota-se que existem 2 variáveis livres x e y, portanto, dim A = 2. Para encontrar uma base, faça x = 1 e y = 0, e posteriormente x = 0 e y =1. Daí, uma base pode ser {(1,0,4), (0,1,0)}.
(b) V = , B = {(x,y,z)/ x = 5y e z = y}
Solução:
B = {(5y ,y,y)}, dim B = 1 e uma base de B é {(5,1,1)}.
(c) V = , C = {(x,y,z)/ x = 0, y = 2x, z = -y}
Solução:
C = {(0,2x,-2x)}, dim C = 1 e uma base de C é {(0,2,-2)} ou {(0,1,-1)}
(d) V = , D = {(x,y,z)/ x +y –z = 0}
Solução:
D = {(x, y, x+y)}, dim D = 2 e uma base de D é {(1, 0, 1), (0, 1, 1)}
(e) V = , E = 
Solução:
E = 
, dim E = 2 e uma base de E é 