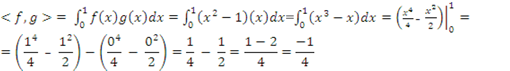Produto interno em espaços vetoriais
Chama-se produto interno no espaço vetorial V uma aplicação de VxV em 
que a todo par de vetores (u,v) 
associa um número real, indicado por u.v, ou ainda, <u,v> , tal que dados 
e 
, os axiomas seguintes sejam verificados:
P1) 
P2)
P3)
P4)
- O número real <u,v> é chamado produto interno dos vetores u e v.
- Note que existe uma diferença na notação: 0 (vetor zero) e 0 (escalar zero)
I)
II)
III)
IV)
Exemplo:
Seja 
e dados 
elementos de V, então o número real 
é um produto interno?
Verificação:
Dados 
elementos de V, então
P1) 
(Verificado)
P2) Se 
, então
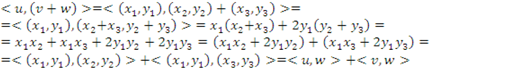
P3) Seja 
, então
(Verificado)
P4) Se 
, então
(i)
(Verificado)
(ii)
(Verificado)
Portanto, 
é um produto interno.
Alguns exemplos de produto interno usual:
1) Se 
, então
De um modo geral.
3) Se 
, então 
Problemas:
1) Sejam os vetores 
pertencentes ao espaço vetorial 
.
Determine o produto interno , considerando o produto interno:
a) 
b)
Solução:
1-a) 
1-b)
2) Seja V = P2o espaço vetorial (espaço dos polinômio de grau menores ou iguais a 2) e o produto interno 
, em que 
. Determine o produto interno de 
.
Solução:
3) Seja V o espaço das funções contínuas no intervalo [0,1] munido do produto interno 
. Determine o produto interno de 
.
Solução:
