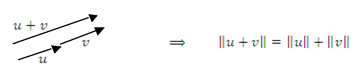Módulo de um vetor
Dado um vetor v de um espaço euclidiano V , chama-se módulo, norma ou comprimento de v, o número real não-negativo, indicado por 
, definido por 
.
Assim, se 
espaço vetorial com produto interno usual, temos que a norma de v é 
Se
, isto é, <v,v>=1, o vetor é unitário. O vetor
é unitário (chamado também de versor). Diz-se, neste caso, que o vetor v foi normalizado.
Exemplos:
1) Dado o vetor v = (1,2,3) pertencente ao espaço vetorial 
, calcular a norma de v e determinar um vetor w que seja unitário (versor) e que tenha a mesma direção e sentido que v, considerando o produto interno:
a) 
(usual), sendo 
.
b) 
, sendo 
.
Solução:
1a) 
é o versor de na norma usual
1b) 
é o versor de v na norma 
É importante observar que o módulo de v depende do produto interno utilizado. Se o produto interno muda, o módulo se modifica.
Os vetores w, obtidos em “a” e “b” são unitários em relação ao respectivo produto interno.
Propriedades da norma de um vetor
Seja um espaço vetorial euclidiano V, então 
:
I) 
II) 
, em que 
III) 
Esta última é conhecida como “desigualdade de Schwarz”, ”inequação de Cauchy-Schwarz” ou também como “desigualdade triangular”.
Interpretação geométrica no 
ou 
.
“A soma de dois lados de um triângulo é maior que a medida do terceiro lado”.
Exemplo:
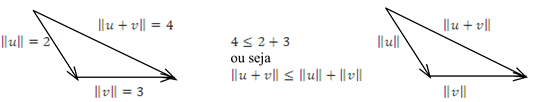
Se os vetores forem colineares, ou seja,
