Ângulo entre dois vetores
Sejam os vetores não-nulos 
um espaço vetorial euclidiano. Podemos definir um ângulo entre dois vetores da seguinte forma:
em que o ângulo 
é um valor real tal que 
.
Exemplos:
1) Considerando o produto interno usual no 
, calcule o ângulo entre os vetores 
e 
.
Solução:
Portanto, 
, daí 
, ou seja, os vetores u e v são ortogonais.
2) Considerando o produto interno usual no 
, calcule o ângulo entre os vetores u = (2, 1, 1) e v = (-1, 2, 1).
Solução:
Portanto 
3) No espaço vetorial das matrizes quadradas V = M(2,2) , dadas duas matrizes quaisquer 
, definimos o produto interno por 
. Sendo 
, calcular o ângulo entre u e v.
Solução:
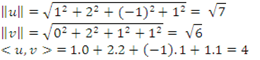
Portanto, 