Vetores ortogonais
Dado um espaço euclidiano V, dizemos que dois vetores u e v pertencentes ao espaço vetorial V são ortogonais e representamos por 
, se, e somente se, <u,v> = 0.
O vetor
é ortogonal a qualquer vetor
.
Se
, então
.
Se
, então
.
Exemplos:
1) Verifique que os vetores u = (3, -3) e v = (2,2) são ortogonais no espaço 
com o produto interno usual.
Verificação:
2) Verifique que os vetores 
são ortogonais no espaço vetorial 
com o produto interno 
, em que 
, mas não é com o produto interno usual.
Verificação:
- Produto interno não-usual:
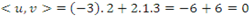(ortogonal) - Produto interno usual:
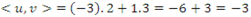(não-ortogonal)