Base ortogonal: base ortonormal
Uma base 
de um espaço vetorial euclidiano V é ortogonal, se os seus vetores são dois a dois ortogonais.
Se dim V = n, qualquer conjunto de n vetores não nulos e dois a dois ortogonais, constitui uma base ortogonal.
O conjunto
é uma base ortogonal do espaço vetorial euclidiano
.
Base ortonormal
Uma base 
de um espaço vetorial euclidiano V é ortonormal, se 
é ortogonal e todos os seus vetores são unitários com relação ao seu produto interno, isto é:
Algumas bases canônicas em relação ao produto interno usual de cada espaço vetorial:
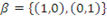é base canônica do espaço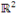 
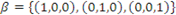é base canônica do espaço 
.
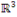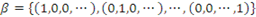é base canônica do espaço 
.
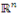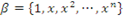é base canônica do espaço Pn.
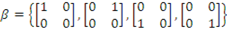é base canônica do espaço M (2,2).
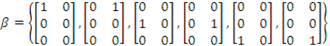é base canônica do espaço M (3,2).
Mais exemplos de bases, agora bases não-canônicas:
- A base
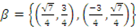é base ortonormal do espaço 
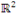em relação ao produto interno usual. - A base
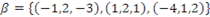é base ortogonal do espaço 
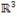em relação ao produto interno usual.
Verificação dos dois últimos exemplos:
Como 
,
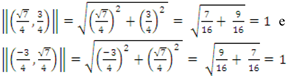
então a base 
é ortonormal do espaço 
em relação ao produto interno usual.
Como 
,
então a base 
é ortogonal do espaço 
em relação ao produto interno usual.
Exemplo:
Dado o vetor 
pertencente ao espaço das matrizes quadradas de ordem 2. Normalizar o vetor v usando o produto interno 
considerando 
.
Solução:
Então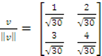 
é um vetor unitário em relação ao produto interno dado.
Processo de ortogonalização de Gram-Schmidt
Dado um espaço vetorial euclidiano V e uma base qualquer 
desse espaço, é possível, a partir dessa base determinar uma base ortogonal de V.
A base ortogonal 
é assim conseguida:
i) Faça w1 = v1 .
ii) Determine 
, em que 
iii) Determine 
, em que 
Seguindo, temos:
n-ésima) Determine 
, em que 
Exemplos:
1) Seja a base não-ortogonal 
do espaço 
em relação ao produto interno usual. Determine uma base β' que seja ortogonal para o espaço .
Solução:
i) 
ii)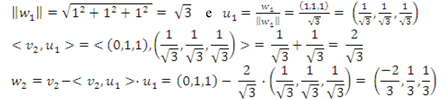
iii)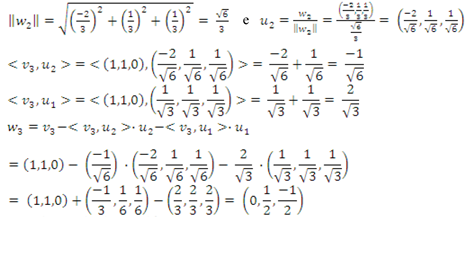
Portanto, a base 
é uma base ortogonalizada a partir da base 
do espaço 
.
Caso queira uma base ortonormal, é só dividir os vetores da base
pelas suas respectivas normas.