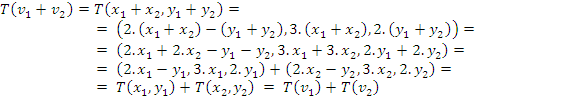Transformações lineares
Seja ![]() e
e ![]() espaços vetoriais. Uma aplicação
espaços vetoriais. Uma aplicação ![]() é chamada transformação linear de
é chamada transformação linear de ![]() em
em ![]() , se
, se
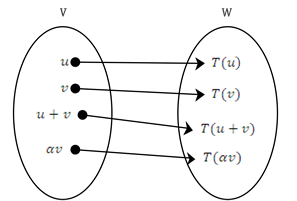
Uma transformação linear de ![]() em
em ![]() (caso em que
(caso em que ![]() ) é chamado de operador linear sobre
) é chamado de operador linear sobre ![]() .
.
Exemplos:
1) Mostre que a aplicação ![]() tal que
tal que ![]() é uma transformação linear.
é uma transformação linear.
Demonstração:
I) Sejam os vetores
e
do espaço vetorial
. Então:
II) Seja
e
. Então,
Portanto, T é uma transformação linear.
2) A transformação identidade ![]() é linear.
é linear.
Demonstração:
3) A transformação nula ![]() é linear.
é linear.
Demonstração: