Interpretação geométrica
A interpretação geométrica de uma transformação linear pode ser dada considerando, por exemplo, o operador linear ![]() tal que
tal que ![]() .
.
- Se
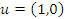 e
e 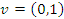 , temos que
, temos que 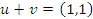
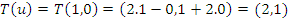
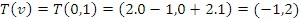
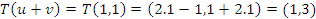
- Se
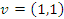 e
e 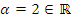 , então
, então 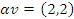
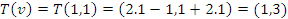
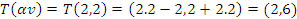
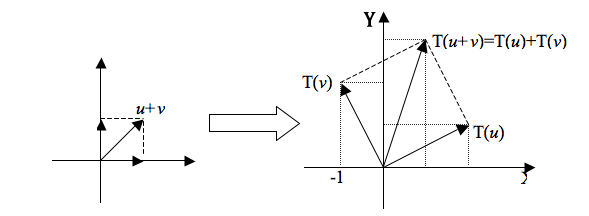
Sendo a diagonal ![]() do paralelogramo determinado por
do paralelogramo determinado por ![]() e
e ![]() , sua imagem
, sua imagem ![]() representa a diagonal do paralelogramo determinado por
representa a diagonal do paralelogramo determinado por ![]() e
e ![]() , isto é,
, isto é, ![]() .
.
Dizemos, neste caso, que ![]() preserva a adição de vetores.
preserva a adição de vetores.
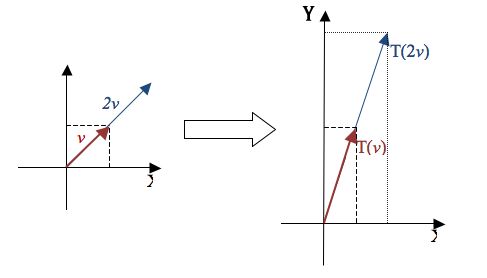
A figura mostra que, ao multiplicarmos o vetor ![]() por
por ![]() , por exemplo, sua imagem
, por exemplo, sua imagem ![]() também fica multiplicada por 2, isto é,
também fica multiplicada por 2, isto é, ![]() .
.