Propriedades das transformações lineares
I) Se 
é uma transformação linear, a imagem do vetor 
é o vetor 
.
Esta propriedade decorre da condição (II) 
da definição de transformação linear, é só fazer 
, temos 
.
Conclusão:
Se 
, a transformação não é linear, É o caso da transformação 
, tal que 
, pois 
.
II) Se 
é uma transformação linear, temos que:
, 
e 
, isto é, a imagem de uma combinação linear de vetores 
é uma combinação linear das imagens 
com os mesmos coeficientes 
.
Se 
é uma base de 
, para todo 
, existe 
tal que 
, e portanto, 
, isto é, dado 
, o vetor 
estará determinado se forem conhecidos as imagens dos vetores de 
.
Em outras palavras, sempre que forem dados 
, onde 
é base do domínio de 
, a transformação de 
está perfeitamente definida.
Exemplo:
Seja 
uma transformação linear e 
uma base do 
. Sabendo que 
, 
e 
, determine:
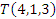.- a lei que determina a transformação linear.
Solução:
1-a) Como 
, então 
, ou de outra forma:
, 
, 
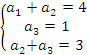
Portanto:
1-b) Da mesma forma que o item anterior, apenas tomando um ponto genérico 
, então 
, ou de outra forma:
, 
, 
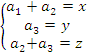
Portanto:
Matriz de uma transformação linear
Seja 
uma transformação linear, 
uma base de 
e 
uma base de 
. Um vetor 
pode ser expresso por:
ou 
e a imagem 
por:
ou
Como 
é linear, temos:
Sendo 
, 
, 
, 
vetores de 
, podemos escrevê-los como:
Reescrevendo 
:
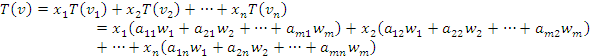
ou
(2)
Comparando-se (1) e (2), temos:
Ou na forma matricial:
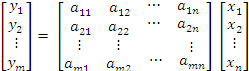
ou simplesmente:
, sendo a matriz 
, denominada matriz de 
em relação as bases 
e 
.
A matriz
é de ordem
quando
e
, onde cada coluna é formada pelos componentes das imagens dos vetores de
em relação à base
:
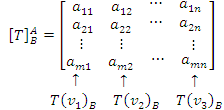
Exemplo:
Seja 
uma transformação linear dada por 
. Considerando a base 
do espaço 
e 
, determine matriz da transformação linear em relação as bases 
e 
.
Solução:
A matriz é de ordem 
, ou seja:
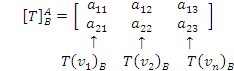
e 
e 
e 
Portanto: 