Propriedades do núcleo e da imagem
- O núcleo de uma transformação linear
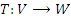é um subespaço vetorial de 
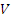. - A imagem de uma transformação linear
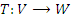é um subespaço vetorial de 
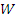. - Se
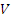é um espaço vetorial de dimensão finita e 
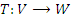uma transformação linear, então 
.
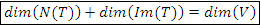Podemos verificar as propriedades, observando os exemplos acima na qual o núcleo 
é um subespaço vetorial de 
com dimensão igual a 1 e a imagem Im
é um subespaço vetorial de 
com dimensão igual a 2.