Introdução
Dada uma transformação linear 
, estamos interessados em saber que vetores (não nulos) são levados em um múltiplo de si mesmo; isto é, procuramos um vetor 
e um escalar 
real tais que
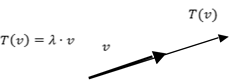
Neste caso 
será um vetor de mesma “direção” que v. O escalar
será chamado autovalor e o vetor 
um autovetor. Vamos formalizar este conceito.
Definição e exemplos
Definição:
Seja 
uma transformação linear. Se existirem 
tais que 
, então 
é um autovalor de 
um autovetor de 
associados a .
Observe que 
pode ser o número 0, embora 
não possa ser o vetor nulo.
Exemplo 1:
Seja 
dado por 
. Neste caso 
= 2 é o autovalor de T e qualquer vetor (x, y) 
(0, 0) é um autovetor de T associado a 
=2.
Exemplo 2:
Seja 
em que T(x,y) = (x, -y).
Note que T(0, -y)=(0,-y)=-1(0, y). Portanto,
=-1 é o autovalor de T e todo vetor v1=(0,y) tal que y 0 é um autovetor de T.
Observe que T(x,0)=(x,0)=1(x,0), então,
=1 é o autovalor de T e todo vetor v2=(x,0) tal que x
0 é um autovetor de T.
Exemplo:
Nos exemplos 1 e 2, quais são as matrizes A1 e A2 associadas às transformações lineares em relação à base canônica?
Solução:
1) A matriz associada deve ser da forma 
. Como
Portanto: 
2) Aqui também, a matriz associada deve ser da forma 
. Como
Portanto: 
As noções de autovetor e autovalor de uma transformação linear (ou matriz) são fundamentais, por exemplo, em Física Atômica os níveis de energia dos átomos e moléculas são dados por autovalores de determinadas matrizes. Também o estudo dos fenômenos de vibração, a análise de estabilidade de um avião e muitos outros problemas de Física leva à procura de autovalores e autovetores de matrizes.