Determinação dos autovalores e autovetores

Autovalores e autovetores de uma matriz

Lembre-se que toda transformação linear está associada a uma matriz em relação à base canônica, isto é, T(v) = A.v.

Logo, o autovalor e autovetor de A é o autovalor e autovetor de T.

Portanto, o autovalor e o autovetor v, são soluções da equação T(v) = v, isto é , , em que (v vetor não nulo).

Dada uma matriz . Para encontrar os autovalores de A, calcula-se o determinante , em que é a matriz identidade.

Polinômio característico

Método prático para encontrar autovalores e autovetores de uma matriz.

Exemplo:

Dado , vamos procurar vetores v=(x,y) não nulo e escalares tais que .

Observe que, se I for a matriz identidade de ordem 2, então a equação acima pode ser escrita na forma

Voltando ao exemplo, temos:

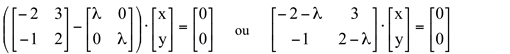
Esta última relação representa um sistema de equações lineares de 2 equações e 2 incógnitas na forma matricial. Como o sistema é de ordem 2x2, uma maneira de resolver é usando a Regra de Cramer.

Se o determinante da matriz dos coeficientes for diferente de zero, então o sistema tem uma única solução, que é a solução nula, ou seja, x=y=0.

Como estamos interessados em calcular os autovetores de A, isto é, vetores v0, queremos que o sistema seja possível e indeterminado, ou seja,

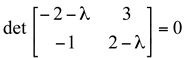
Portanto, .

Denominamos de polinômio característico da matriz A ao polinômio definido por .

Obs.:

Continuando a resolução, temos , que são as raízes do polinômio característico e, portanto, os autovalores da matriz A são -1 e 1.

Através dos autovalores encontramos os autovetores.

(I) Substituindono sistema 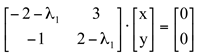, temos:

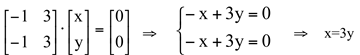
O autovetor associado a é v₁=(3y,y), , ou v₁=(x,x/3), . Ou de outra forma, o autovetor associado a , é todo vetor múltiplo de v₁=(3,1). Assim, v₁=(3,1) é um autovetor que gera o autoespaço de .

(II ) Substituindo no sistema 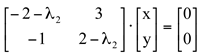, temos:

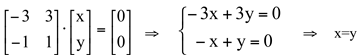
O autovetor associado a é v2=(x,x), . Ou de outra forma, o autovetor associado a , é todo vetor múltiplo de v2=(1,1). Assim, v2=(1,1) é um autovetor que gera o autoespaço de .