Unidade I – Autovalores e Autovetores

Matriz diagonalizável

Temos a melhor situação possível quando uma matriz quadrada é semelhante a uma matriz diagonal. Como veremos logo a seguir, a possibilidade de isso ocorrer está relacionada estreitamente com os autovalores e autovetores da matriz.

Definição:

Uma matriz A(n x n) é diagonalizável se existe uma matriz diagonal D tal que A~D, ou seja, se existe P(n x n)  inversível tal que P^-1AP=D.

Exemplo:

A matriz  é diagonalizável, pois, se , então

Teorema:

A matriz A(n x n) é diagonalizável, se e somente se, A tiver n autovetores LI.

Em outras palavras:

Existe P inversível e uma matriz diagonal D tal que P^-1AP=D se, e somente se, as colunas de P forem n autovetores LI de A, e os elementos da diagonal de D forem os autovalores correspondentes aos autovetores.

Exemplos:

Se possível, determine a matriz P que diagonaliza a seguinte matriz:

a)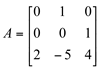                  b)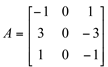

Soluções:

a)

Os autovalores são

Para  tem como autovetor os múltiplos de (1,1,1).

Para  tem como autovetor os múltiplos de (1,2,4).

Como não é possível existirem 3 autovetores LI, pelo teorema anterior, A não é diagonalizável.

Obs:

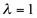•  tem multiplicidade algébrica igual a 2 e  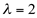tem multiplicidade algébrica igual a 1.
• Cada autovalor gera somente um autovetor, portanto, a multiplicidade geométrica é 1, para qualquer autovalor.

b) 

Para  temos autovetores da forma , que são gerados pelos vetores v₁=(0,1,0) e v₂=(1,0,1).

Para  tem como autovetor v₃=(-1,3,1).

É fácil verificar que estes 3 vetores são LI. Pelo teorema,

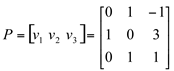 é invertível. Além disso, 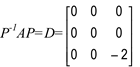, ou que, AP=PD.

Obs:

•  Se 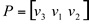 então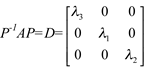
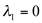• tem multiplicidade algébrica igual a 2 e  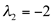tem multiplicidade algébrica igual a 1.
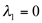• geral dois autovetores e  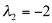gera um autovetor, portanto,  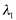tem multiplicidade geométrica igual a 2 e  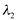tem multiplicidade geométrica igual a 1.

Teorema

Se A(n x n) têm n autovalores distintos entre si, então A é diagonalizável.

Teorema da Diagonalização

Seja A(n x n) com n autovalores distintos (não necessariamente distintos entre si).

São equivalentes os enunciados:

I) A é diagonalizável.
II) A união de todos os autovetores gerados pelos autovalores contém n vetores LI.
III) A multiplicidade algébrica de cada autovalor é igual a sua multiplicidade geométrica.

Exemplos

a)  tem multiplicidade algébrica igual a 2 mas multiplicidade geométrica igual a 1, logo 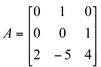 não é diagonalizável, de acordo com o Teorema da Diagonalização.

b) A matriz 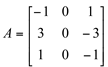 tem dois autovalores distintos . O autovalor tem multiplicidades algébrica e geométrica iguais a 2, e para o autovalor  as multiplicidades são iguais a 1. Portanto, de acordo com o Teorema da Diagonalização, A é diagonalizável.