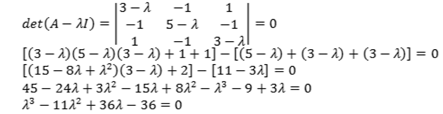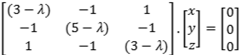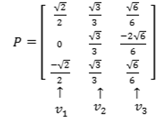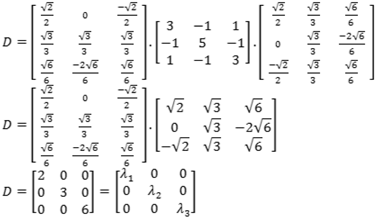Diagonalização de matrizes simétricas
Operador simétrico ou matriz simétrica
Um operador linear é simétrico se a matriz que o representa numa base ortonormal é simétrica, isto é, se 
.
A matriz do operador simétrico é sempre simétrica, independente da base ortonormal do espaço.
Exemplo:
O operador 
tal que T(x,y) = (3x + 2y, 2x - y) é simétrico, pois a matriz canônica de T que é dada por 
é simétrica, isto é, 
.
- A equação característica de uma matriz simétrica tem apenas raízes reais.
- Se
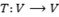é um operador linear simétrico com autovalores distintos, então os autovetores são ortogonais. - Se a matriz A é diagonalizável pela matriz P, ou seja,
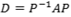, como foi visto, em particular, se a matriz A é simétrica, pela propriedade anterior, P será base ortogonal. - É conveniente, em aplicações, que além de ortogonal, os vetores sejam ortonormais, neste caso, basta normalizar os vetores e teremos bases ortonormais.
- Como as colunas (ou linhas) de uma matriz ortogonal são vetores ortonormais, então os autovetores ortonormais de P formarão uma matriz ortogonal.
- Se
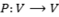é um operador linear ortogonal sobre o espaço euclidiano V. Então, a inversa da matriz de P é a mesma da transposta, isto é, 
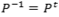. Dessa forma a relação de diagonalização ficará da seguinte forma 
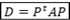e, nesse caso, dizemos que P diagonaliza A ortogonalmente.
Exemplo:
Determinar uma matriz ortogonal que diagonaliza a matriz simétrica 
.
Solução:
I) Determinação dos autovalores:
Soluções possíveis:
Teste:
Para, temos
(F)
Para, temos (-
(F)
Para, temos
(V)
Então, a primeira raiz é.
Fazendo a divisão do polinômio característico por, temos:
Resolvendo a equação de segundo grau, encontramos as outras duas raízes
.
II) Determinação dos autovetores:
O sistema homogêneo é
, ou seja:
a) Para
, temos:
Ou de outra forma:
Portanto,
Fazendo
, temos o autovetor unitário
associado ao autovalor
.
b) Para
, temos:
Ou de outra forma:
Portanto,
Fazendo
, temos o autovetor unitário
associado ao autovalor
.
c) Para
, temos:
Ou de outra forma:
Portanto,
Fazendo
, temos o autovetor unitário
associado ao autovalor
.
III) Formação da matriz ortogonal que diagonaliza a matriz simétrica:
IV) Verificação da diagonalização:
