Polinômio Minimal
Seja A uma matriz quadrada sobre um corpo K, e denotemos por J(A) a coleção de todos os polinômios f(t) para os quais f(A)=0, observe que J(A) não é vazio, pois o polinômio característico 
de A pertence a J(A). Seja m(t) o polinômio mônico de menor grau em J(A), então, m(t) é o polinômio mínimo de A e se tal polinômio existe é único.
Teorema 1:
O polinômio mínimo m(t) de A divide todo polinômio que tem A como zero. Em particular, m(t) divide o polinômio característico 
de A.
Teorema 2:
Os polinômios característicos e mínimo de uma matriz A têm os mesmos fatores irredutíveis.
Este teorema, não nos diz que 
, e sim que qualquer fator irredutível de um deve dividir o outro. Em particular, como um fator linear é irredutível, m(t) e A(t) têm os mesmos fatores lineares; logo eles têm as mesmas raízes, o que poderemos ver no próximo teorema.
Teorema 3:
Um escalar λ é um autovalor de uma matriz A se e somente se λ é uma raiz do polinômio mínimo de A.
Exemplo 1:
Ache o polinômio mínimo m(t) de 
Solução:
Inicialmente, vamos determinar o polinômio característico:
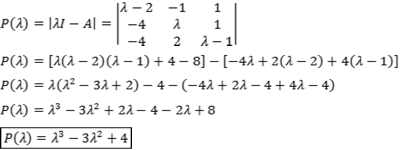
Possíveis raízes: 
Verificação:
Para 
Para 
Então, 
é uma raiz do polinômio.
Fazendo a divisão: 
Podemos determinar as outras duas raízes: 
Portanto, os possíveis polinômios minimais são:
Como o polinômio minimal é o que possui menor grau que se anula com a matriz, então vamos verificar primeiro 
:
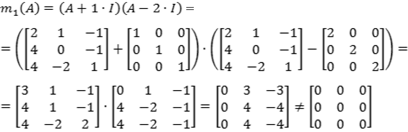
Agora, vamos verificar 
:
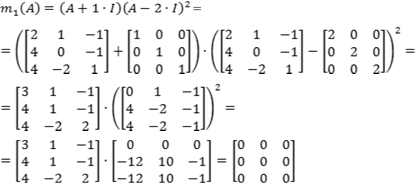
A última verificação não tinha necessidade de fazer, pois o polinômio minimal é no máximo o próprio polinômio característico.
Portanto, o polinômio minimal é 
Operadores nilpotentes
Um operador linear 
é chamado nilpotente se 
para algum inteiro positivo n; k é o índice de nilpotência de T se 
, mas 
. Analogamente, uma matriz quadrada A é chamada nilpotente se 
para algum inteiro positivo n, e de índice k se 
, mas 
. Obviamente o polinômio mínimo de um operador (matriz) nilpotente de índice k é
; logo 0 é seu único autovalor.
Teorema 4:
Seja 
um operador nilpotente de índice k. Então T admite uma representação matricial em bloco cujos elementos diagonais têm a forma:
isto é, todos os elementos de N são 0 (zeros), exceto os que estão, diretamente acima da diagonal principal, e que são 1 (uns). Há ao menos uma matriz N de ordem k, e todas as outras matrizes N são de ordem menores ou igual a k. O número de matrizes N de cada ordem possível é determinado de modo único por T. Além disso, o número total de matrizes N de todas as ordens é igual à nulidade de T.
Observemos que a matriz N acima é ela própria nilpotente, e que seu índice de nilpotência é igual a sua ordem. Note-se que a matriz N de ordem 1 não é mais do que a matriz zero 0(1x1).