Forma canônica de Jordan
Um operador T pode ser posto em forma canônica de Jordan se seus polinômios característico e mínimo puderem fatorar-se em polinômios lineares. Isto é sempre verdadeiro se K é o corpo complexo 
. Em qualquer caso, podemos sempre prolongar o corpo base K para um corpo em que os polinômios mínimo e característico se decompôem, de fato, em fatores lineares; assim, em um sentido amplo, todo operador tem uma forma canônica de Jordan. Analogamente, toda matriz é semelhante a uma matriz em forma canônica de Jordan.
Teorema 5:
Seja 
um operador linear cujos polinômios característico e mínimo são, respectivamente, 
onde os 
são escalares distintos. Então, T admite uma representação matricial em bloco J cujos elementos diagonais têm a forma
Para cada 
os blocos correspondentes 
têm as seguintes propriedades:
- Há ao menos um
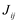de ordem mi; todos os outros 
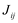são de ordem 
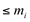. - A soma das ordens dos
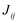é
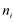. - O número de
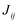é igual à multiplicidade geométrica de 
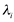. - O número de
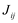de cada ordem possível é univocamente determinado por T.
A matriz J que aparece no teorema acima é chamada forma canônica de Jordan do operador T.
Um bloco diagonal 
é chamado bloco de Jordan pertencente ao autovalor 
.
Observe que:
Isto é 
, onde N é o bloco nilpotente que aparece no Teorema 4:
Exemplo 2:
Suponhamos que os polinômios característico e mínimo de um operador T sejam, respectivamente, 
. Então, a forma canônica de Jordan de T é uma das matrizes seguintes:
A primeira matriz ocorre se T tem dois autovetores independentes pertencentes ao seu autovalor 2; e a segunda matriz ocorre se T tem três autovetores independentes pertencentes a 2.
Exemplo 3:
Determine todas as formas canônicas possíveis para um operador linear 
cujo polinômio característico é
.
Solução:
Exemplo 4:
Determine todas as formas canônicas de Jordan J possíveis para uma matriz de ordem 6 cujo polinômio mínimo é
.
Solução:
