Conjuntos Numéricos Fundamentais
Em nosso cotidiano, frequentemente, fazemos uso dos números que fazem parte de diversas áreas do conhecimento humano. Ao analisarmos um exame de sangue temos uma ideia, por exemplo, de como está nossa taxa de glicemia, que na normalidade, deve variar de 70 a 99. Ao pagarmos uma conta de energia elétrica ou água, uma determinada porcentagem desse valor corresponde a impostos. Em uma compra, podemos decidir se é melhor pagar à vista com desconto ou a prazo, se os juros forem baixos. Percebemos que existe uma quantificação e esta, por sua vez, é expressa por números.
Conjunto dos Números Naturais
Em Matemática, esses números são organizados e classificados em conjuntos numéricos. O primeiro conjunto numérico que a humanidade fez uso foi o Conjunto dos Números Naturais, expresso por IN e que é constituído apenas por números inteiros e positivos:
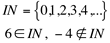
Observa-se que este conjunto possui infinitos elementos, o que é representado pelas reticências (...).
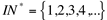
Conjunto dos Números Inteiros Relativos
Mais tarde, ao surgirem as quantidades negativas, foi preciso ampliar este conjunto, criando-se, então, o Conjunto dos Números Inteiros Relativos, indicado por Z, que contém apenas números inteiros positivos, negativos mais o zero:
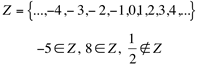
Observa-se que todo o número natural é também um número inteiro relativo.
O conjunto Z apresenta os seguintes subconjuntos:
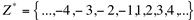ou seja,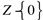 
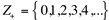conjunto dos números inteiros não negativos.
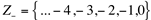conjunto dos números inteiros não positivos.
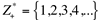conjunto dos números inteiros positivos.
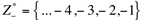conjunto dos números inteiros negativos.
Conjunto dos Números Racionais
Como foi preciso trabalhar também com as quantidades fracionadas, ampliou-se o conjunto Z, construindo-se o Conjunto dos Números Racionais, simbolizado por Q, isto é, o conjunto dos números que podem ser escritos na forma de fração. Este conjunto não pode ser representado por extensão, enumerando-se os seus elementos, pois dado um número racional, não se sabe qual será o próximo. Neste caso, podemos representar os infinitos números racionais por uma propriedade comum a todos eles, ou seja:
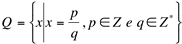
Leia-se: “o conjunto Q é o conjunto formado pelos elementos x tal que x seja igual a uma fração de numerador p e denominador q, onde p é um número inteiro e q um número inteiro diferente de zero”.
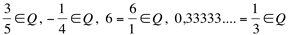
Verifica-se que todo o número inteiro relativo é também um número racional.
Conjunto dos Números Irracionais
Porém, há uma classe de números que não podem ser escritos na forma de fração, pois sua parte decimal é constituída de infinitas casas decimais, sem repetição periódica. Como exemplos:
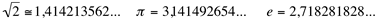
Estes números formam o Conjunto dos Números Irracionais, indicado por I.
Um número não pode ser racional e irracional ao mesmo tempo, ou seja, ou se pode escrevê-lo na forma de fração ou não se pode.
Conjunto dos Números Reais
Pode-se representar por diagramas de Venn os conjuntos IN, Z, Q e I, e verificarmos a relação de inclusão que existe entre eles:
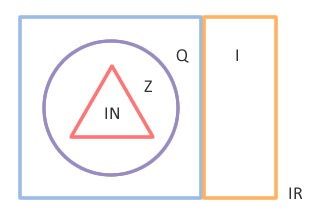
Assim, temos que IN está contido em Z que está contido em Q , em símbolos: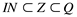
. Ao fazermos a união 
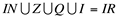, constituímos o Conjunto dos Números Reais.
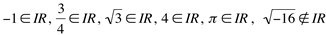
Portanto, qualquer número é um número real, exceto os que resultam de uma raiz de índice par com radicando negativo. Estes fazem parte de uma outra classe de números, que pertencem ao Conjunto dos Números Complexos que no momento, não faz parte do nosso estudo.
É possível fazer uma correspondência biunívoca entre os elementos do conjunto dos números reais e os pontos de uma reta (chamada, então, de reta real). Isto significa que a cada ponto dessa reta corresponde um único número real e a cada número real corresponde um único ponto da reta.
Vejamos então:
