Noção Intuitiva de Limite de uma Função
Tomemos a função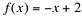 
. Vamos verificar o que acontece com o valor da variável dependente y dessa função quando o valor da variável independente x se aproxima do valor 1, por exemplo. Podemos fazer essa aproximação de duas maneiras distintas: por valores ligeiramente menores que 1 (tanto quanto se deseja) e por valores ligeiramente maiores que 1 (tanto quanto se queira), sem no entanto, fazermos o valor de x exatamente igual a 1.
Para tal, vamos construir uma tabela, fazendo os valores de x próximos de 1, pela direita (valores ligeiramente maiores que 1):
x |
f(x)=-x+2 |
2 |
f(1)=-2+2=0 |
1,5 |
f(1,5)=-1,5+2=0,5 |
1,21 |
f(1,21)=-0,21+2=0,79 |
1,01 |
f(1,01)=-1,01+2=0,99 |
1,00001 |
f(1,00001)=-1,00001+2=0,99999 |
Verifica-se que quando x se aproxima de 1, por valores ligeiramente maiores que 1 , y se aproxima de 1. Em notação matemática, tem-se:
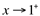. (Leia-se: x tende a 1 pela direita);;; . 
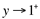(Leia-se: y tende a 1 pela direita);
Diz-se, então que o limite lateral de f(x) quando x se aproxima de 1 pela direita é igual a 1 e denota-se: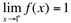 
De outra forma, podemos construir uma tabela, fazendo os valores de x próximos de 1, pela esquerda (valores ligeiramente menores que 1):
x |
f(x)=-x+2 |
0 |
f(0)=-0+2=2 |
0,5 |
f(0,5)=-0,5+2=1,5 |
0,71 |
f(0,71)=-0,71+2=1,29 |
0,95 |
f(0,95)=-0,95+2=1,05 |
0,99999 |
f(0,99999)=-0,99999+2=1,00001 |
Nota-se que quando x se aproxima de 1, por valores ligeiramente menores que 1 , y se aproxima de 1. Em notação matemática, tem-se:
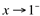. (Leia-se: x tende a 1 pela esquerda);. 
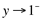(Leia-se: y tende a 1 pela esquerda);
Diz-se, então que o limite lateral de f(x) quando x se aproxima de 1 pela esquerda é igual a 1 e denota-se: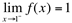 
.
Convém destacar que essas aproximações são infinitesimais e que x nunca assume o valor exatamente igual a 1.
O gráfico abaixo, da função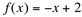 
ilustra bem esta situação:
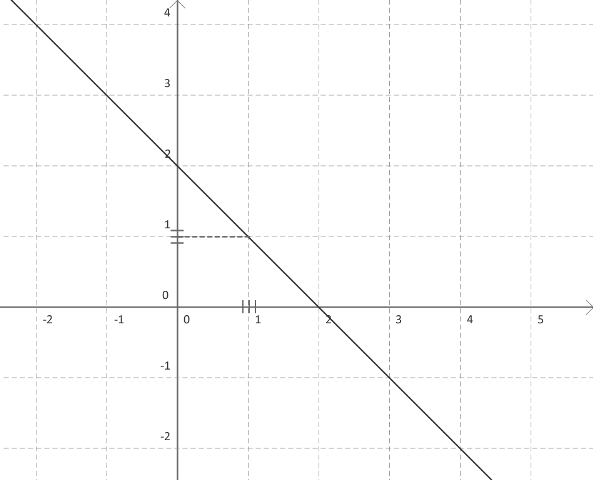
Como os limites laterais são iguais, conclui-se, então que o limite de f(x) quando x se aproxima de 1 é igual a 1 e denota-se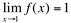 
.