Relação entre Valor Numérico e Limite
Por definição, valor numérico e limite de uma função são conceitos diferentes. Por isso, a relação entre eles se dá de três maneiras como se vê nos seguintes exemplos:
Ex1. f(x) está definida em “a” e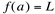 
.
Se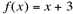 
, então 
.
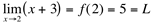Ex2 f(x) está definida em “a” , mas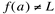 
.
Se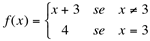 
então 
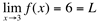e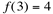 
.
Ex3 f(x) não está definida em “a”:
Se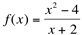 
, então 
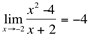,mas observa-se que 
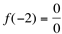o que é uma indeterminação, ou seja, 
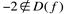. Mas, por outro lado, este limite existe, sendo 
.
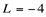Vejamos, agora dois teoremas sobre limites:
Teorema da Unicidade do Limite
Se o limite de uma função f existir, então é único.
Teorema da Existência do Limite
Se f é definida em todo intervalo aberto I contendo “a”, exceto possivelmente o próprio “a”, então existe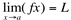 
, se e somente se 
.
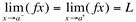Isto significa dizer, informalmente, que o limite de uma função só existe se os seus limites existirem e forem iguais.