Limites Indeterminados
No cálculo de limites, é comum aparecerem expressões do tipo:
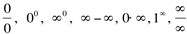
Diz-se que estas expressões são indeterminadas. Para esclarecer esta questão, vejamos os seguintes exemplos:
Ex1: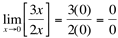
, ou seja, a divisão de zero por zero, dependendo das funções, pode ser qualquer valor real ou até mesmo não existir.
Como não nos interessa o valor numérico da função para quando x assume o valor 0, mas sim o que acontece com a função quando x se aproxima de 0, podemos usar artifícios algébricos para calcular o limite em questão:
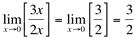(neste caso, houve uma simplificação do numerador com o denominador da função).
Ex2: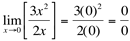
Simplificando-se o numerador e o denominador temos que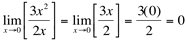 
.
A seguir vejamos mais alguns casos de limites indeterminados que podem ser revolvidos por artifícios algébricos:
Ex3: Calcule :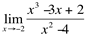
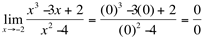(indeterminação!)
Neste caso, como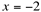 
além de ser o valor da tendência, é também a raiz do polinômio do numerador e do polinômio do denominador, é possível simplificá-los, dividindo-os por 
.
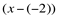Outra forma de simplificação, que é mais rápida que a anterior é usar o dispositivo de Briot-Ruffini. Significa decompor esses polinômios em um produto de outros polinômios de grau menor.
Aplicando Briot-Ruffini para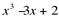 
, tem-se que:
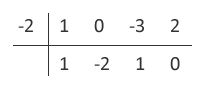
Logo,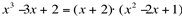
Usando Briot-Ruffini para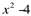 
, tem-se que:
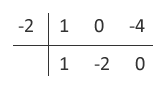
Logo,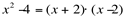
Podemos, então, calcular o limite, da seguinte forma:
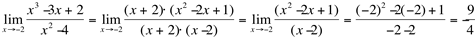
Ex4: Calcule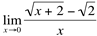 
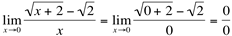(indeterminação!)
Neste caso, podemos resolver este limite, multiplicando o numerador e o denominador pelo conjugado da expressão que traz a diferença de duas raízes quadradas.
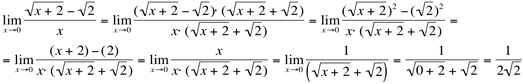
Ex5: Calcule o valor de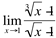 
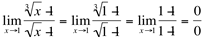(indeterminação!)
A solução para esse tipo de limite, que possui raízes de índices diferentes, porém com o mesmo radicando, é fazermos uma substituição de variável da seguinte maneira: substituímos o radicando por uma variável qualquer, elevado a um expoente que é o m.m.c. (mínimo múltiplo comum) dos índices das raízes.
Então fazemos:
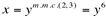, mas esta substituição pode alterar o valor da tendência da variável x do limite. Ou seja, quando 
.
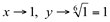Assim, reescrevemos o nosso limite, na variável y:
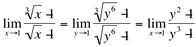
Observe que agora, o limite ainda continua indeterminado, mesmo com mudança de variável. A vantagem é que podemos resolvê-lo como o limite do exemplo 3, aplicando o dispositivo de Briot-Ruffini:
