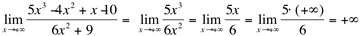Limites no Infinito
Observe o gráfico da função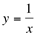 
.
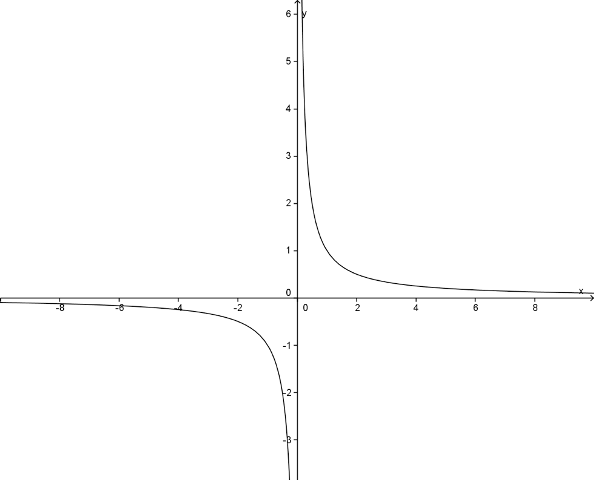
Note que quando x tende ao mais infitinto, os valores de y tendem a zero e quanto x tende ao menos infinito, os valores de y também tendem a zero.
Em símbolos podemos representar assim:
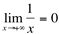e 
E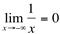stes limites são exemplos de limites no infinito, cuja definição formal apresentamos a seguir:
Definição 1: Seja f uma função definida em um intervalo aberto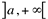 
. Escrevemos 
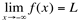quando o número L satisfaz à seguinte condição:
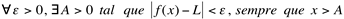. Significa dizer que a partir de um determinado valor A, positivo, a função se estabiliza em torno do valor L.
Definição 2: Seja f uma função definida em um intervalo aberto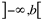 
. Escrevemos 
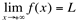quando o número L satisfaz à seguinte condição:
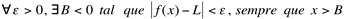. Significa dizer que a partir de um determinado valor B, negativo, a função se estabiliza em torno do valor L.
Operações com Limites Infinitos:
Supondo que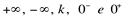 
sejam resultados de limites de funções, as seguintes situações podem ocorrer:
A seguir apresentamos dois teoremas que serão muito úteis na resolução de limites infinitos.
Teorema 1: Se n é número inteiro positivo, então são válidos:
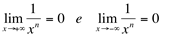
Teorema 2: Sejam os polinômios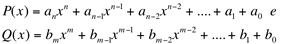 
então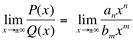 
.
Ex. Calcule o seguinte limite, usando os dois teoremas: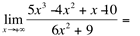 
Solução:
Usando o Teorema 1:
Colocam-se os termos de maior grau da variável em evidência, no numerador e no denominador.
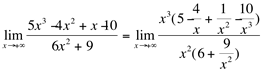
Desta forma, os termos que estão dentro dos parênteses, com denominador na variável x, tendem a zero.
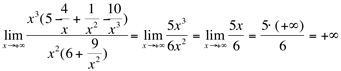
Usando o Teorema 2:
Basta usar os termos de maior grau da variável no numerador e no denominador, desprezando-se os demais.
