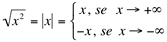Limites Infinitos
No caso, são limites cujo resultado é o infinito.
Observe o gráfico da função 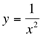 .
.
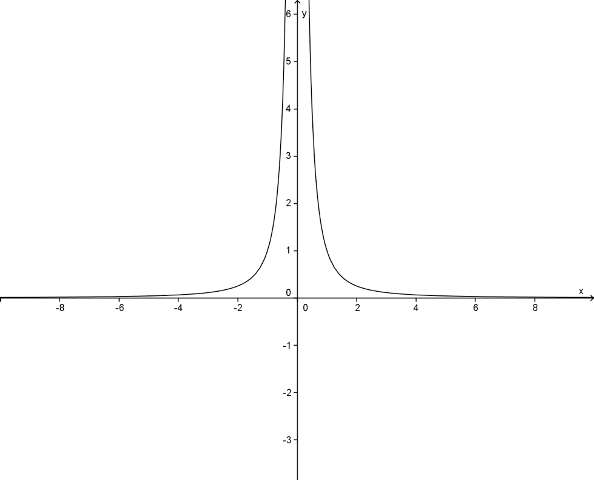
Note que quando os valores de x se aproximam de 0, pela esquerda, os valores de y tendem ao mais infinito. E quando os valores de x se aproximam de 0, pela direita, os valores de y também tendem ao mais infinito. Em simbologia matemática, temos:
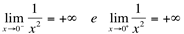 (limites laterais da função)
(limites laterais da função)
Como os limites laterais são iguais, então o limite da função existe:
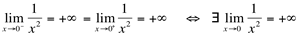
Definição 1: Seja f uma função definida em um intervalo aberto contendo “a”, exceto, possivelmente, em 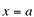 . Diz-se que
. Diz-se que 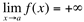 , se para qualquer A>0, existir um
, se para qualquer A>0, existir um 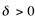 tal que f(x)>A sempre que
tal que f(x)>A sempre que 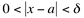 .
.
Definição 2: Seja f uma função definida em um intervalo aberto contendo “a”, exceto, possivelmente, em 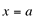 . Diz-se que
. Diz-se que 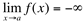 , se para qualquer B<0, existir um
, se para qualquer B<0, existir um 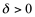 tal que f(x)<B sempre que
tal que f(x)<B sempre que 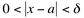 .
.
Teorema: Se n é um número inteiro positivo qualquer, então:
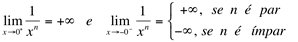
Ex1: Calcule 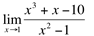
Solução:
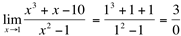 Este resultado nos leva a pensar que o resultado desse limite se reduz a três possibilidades: não existir, ser
Este resultado nos leva a pensar que o resultado desse limite se reduz a três possibilidades: não existir, ser 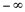 ou ser
ou ser 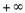 .
.
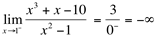 e
e 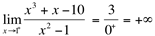
Como os limites laterais são diferentes, então 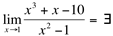 , ou seja, não existe este limite.
, ou seja, não existe este limite.
O gráfico abaixo, da função 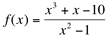 ilustra bem esta situação:
ilustra bem esta situação:
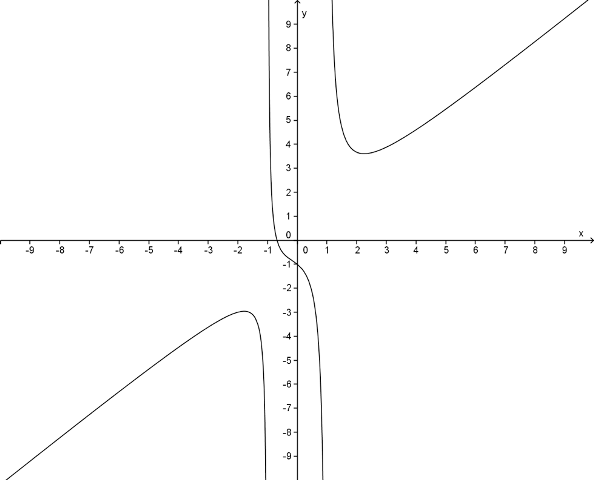
Ex2. Indeterminações da forma 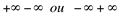 .
.
Calcule : 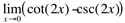
Ao fazermos a substituição da variável pelo valor da tendência, tem-se:
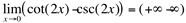 (indeterminação)
(indeterminação)
Solução: reduzir a uma só fração:
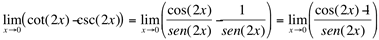
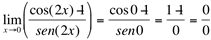 (indeterminação)
(indeterminação)
Multiplicando-se o limite pelo conjugado de (cos(2x)-1), tem-se:
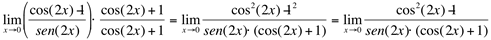
Lembrando que 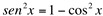 , então
, então 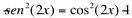 :
:
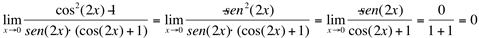
Ex3. Calcule 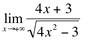
Solução:
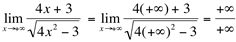 (indeterminação)
(indeterminação)
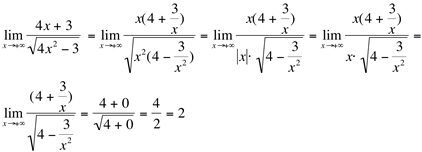
| ||||
|