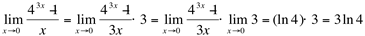Limites Fundamentais
São assim chamados porque apresentam casos especiais de indeterminações do tipo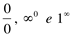 
.
Podemos agrupá-los em quatro casos distintos:
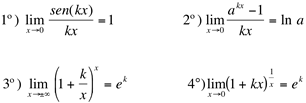
Onde e representa o número de Euler: e=2,718...e k uma constante real.
A verificação desses limites fundamentais pode ser feita facilmente traçando os gráficos das respectivas funções e verificando em torno do valor da tendência, o que acontece com a função.
Como ilustração, observe o gráfico da função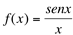 
:
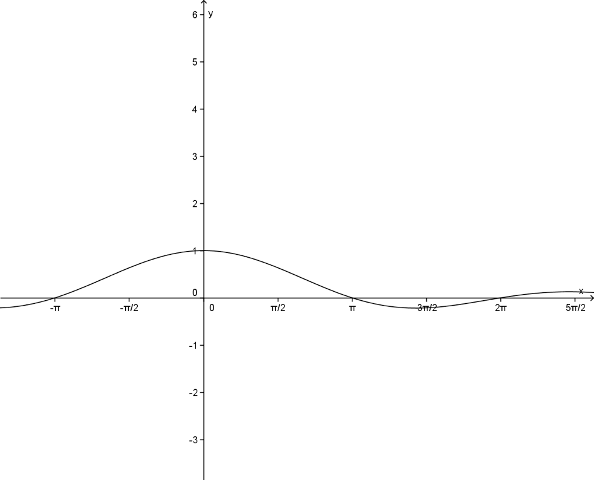
Repare que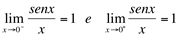 
(limites laterais iguais).
Então,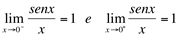
Ex1. Calcule o valor de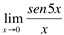 
Solução:
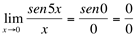(indeterminação)
Para ser um limite fundamental do 1° caso, devem acontecer duas condições:
- O valor da tendência deve ser tal que faça com que o arco do seno tenda a zero.
- A expressão algébrica do arco deve ser idêntica à expressão algébrica do denominador
Este exemplo 1 é um limite indeterminado, mas não é um limite fundamental, pois falha a segunda condição: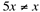 
Para resolvê-lo, vamos transformá-lo em um limite fundamental:
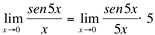(divide-se o denominador por 5 e multiplica-se o numerador também por 5 para não alterar o valor do limite).
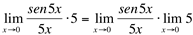(propriedade operatória do limite)
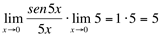
Ex2. Calcule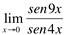 
Resolução:
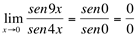(indeterminação)
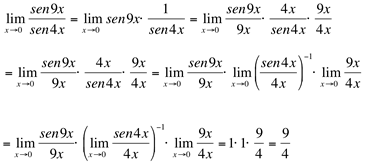
Ex3. Calcule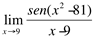 
Resolução:
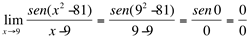(indeterminação)
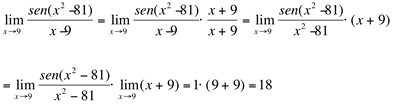
Ex4. Calcule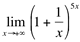 
Resolução:
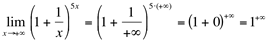(indeterminação)
Para transformar esse limite em um limite fundamental, usamos artifícios algébricos:
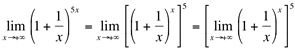(propriedades operatórias das potências e dos limites).
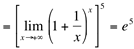
Ex5. Calcule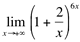 
Resolução:
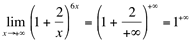(indeterminação)
Neste caso, como precisamos trabalhar na base da função, fazemos uma substituição de variável para chegarmos ao limite fundamental:
Fazendo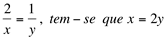 
; Quando 
.
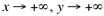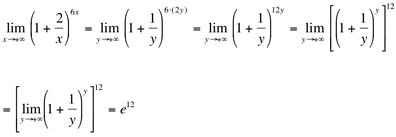
Ex6. Calcule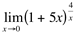 
Resolução:
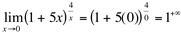(indeterminação)
Para resolvê-lo, fazemos a seguinte substituição de variável:
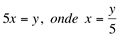; Quando 
.
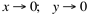Então: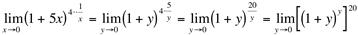 
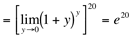
Ex7. Calcule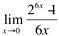 
Resolução:
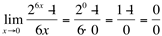(indeterminação)
Observe que este limite é um limite fundamental, pois apresenta duas características:
- a variável (x) tende para um valor que torna nulo o expoente da base (2).
- a expressão algébrica do expoente da base (6x) é idêntica ao denominador (6x)
Então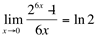 
Ex8. Calcule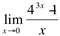 
Resolução:
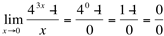(indeterminação)
É possível transformar esse limite em um limite fundamental por meio de manipulações algébricas:
