Continuidade de Funções
Empiricamente, identifica-se uma função contínua, quando ao plotarmos o seu gráfico, em um sistema cartesiano ortogonal, por exemplo, observa-se que todos os seus pontos são unidos por uma curva contínua. Isto é, a função não “salta” de um ponto para outro.
Como exemplo, de função contínua, observe o gráfico da função 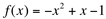
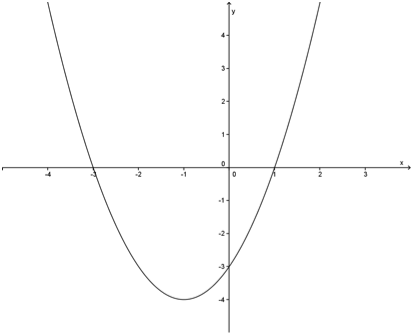
Veja que a função é definida para todos os infinitos pontos do seu domínio.
Como contraexemplo, observe o gráfico de 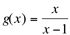
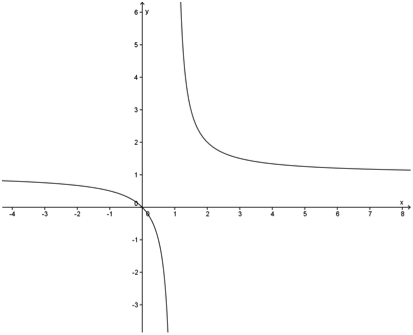
Veja que a função não é definida para 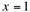 .Além disso, quando os valores de x se aproximam de 1, pela esquerda, os valores de y tendem para
.Além disso, quando os valores de x se aproximam de 1, pela esquerda, os valores de y tendem para 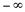 e quando os valores de x se aproximam de 1, pela direita, os valores de y tendem para
e quando os valores de x se aproximam de 1, pela direita, os valores de y tendem para 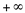 .Ou seja, em torno do valor
.Ou seja, em torno do valor 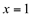 , a função “salta” de
, a função “salta” de 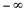 para
para 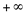 e, portanto, não é contínua em
e, portanto, não é contínua em 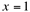 .
.
Convém salientar que a continuidade de uma função é analisada ponto a ponto, ou em um intervalo específico. Uma função pode não ser contínua em um ponto e ser contínua em outro. É o que acontece com o exemplo anterior: a função 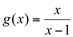 Apresenta descontinuidade somente em
Apresenta descontinuidade somente em 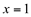 .
.
Definição 1:
Uma função f é contínua em um ponto “a” se forem satisfeitas as seguintes condições:
1ª) f é definida em algum intervalo aberto contendo o ponto “a”. Isto significa dizer que “a” pertence ao domínio de f e, portanto existe f(a).
2ª) Existe 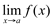 , ou seja, os limites laterais existem são iguais e finitos.
, ou seja, os limites laterais existem são iguais e finitos.
3ª) 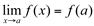 , ou seja, o limite da função f quando x tende para “a” dever ser igual ao valor numérico da função no ponto
, ou seja, o limite da função f quando x tende para “a” dever ser igual ao valor numérico da função no ponto 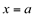 .
.
Quando uma função não é contínua em “a”, dizemos que estão função é descontínua em “a” ou que apresenta uma descontinuidade em “a”.
Se a primeira condição falhar, isto é , “a” não for um ponto que pertence ao domínio da função, então não há sentido em dizer se a função é contínua ou descontínua nesse ponto.
Teorema da Continuidade
Se uma função f é definida em um intervalo aberto “a”, então f é contínua em “a”, se para cada 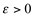 , existe um
, existe um 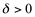 , tal que
, tal que 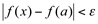 sempre que
sempre que 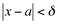 .
.
Ex1. Usando as condições de continuidade, verifique se a função 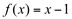 é contínua no ponto
é contínua no ponto 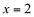 .
.
Solução:
Verificando as condições de continuidade:
1ª) 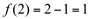 (o ponto
(o ponto 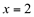 pertence ao domínio de f)
pertence ao domínio de f)
2ª) 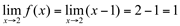
3ª) 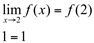
Como as três condições foram satisfeitas, conclui-se que a função 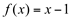 é contínua em
é contínua em 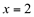 .
.
Observe o gráfico dessa função:
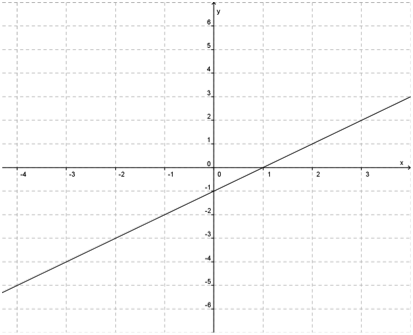
Essa função é contínua para qualquer ponto do seu domínio.
Ex2. O mesmo para a função 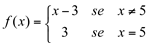 no ponto
no ponto 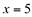
Solução:
1ª) 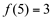
2ª) Esta função é definida por mais de uma sentença, então vamos calcular os limites laterais:
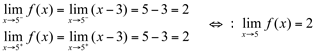
3ª) 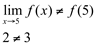
Como a terceira condição falhou esta função não é contínua em 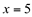 .
.
Veja, abaixo, o gráfico dessa função:
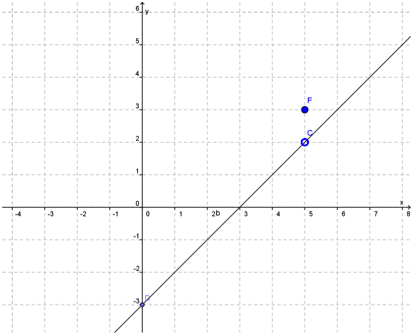
Repare que o gráfico desta função é uma reta que dá um salto em 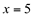 .
.
Ex3. O mesmo para a função 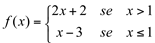 em
em 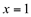 .
.
Solução:
1ª) 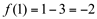
2ª) 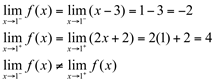
Como a segunda condição falhou esta função não é contínua em 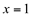 .
.
Observe o gráfico dessa função:
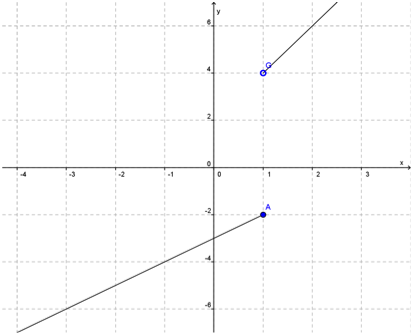
Note que em torno do ponto 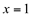 a função dá um “salto”.
a função dá um “salto”.