Definição de Derivada de uma Função
Observe o gráfico de uma função .png) ;
;
Marcamos um ponto .png) sobre o gráfico de
sobre o gráfico de .png) . Adicionando-se incrementos
. Adicionando-se incrementos .png) e
e .png) ao ponto
ao ponto .png) , conseguimos o ponto
, conseguimos o ponto .png) Veja que pelos pontos
Veja que pelos pontos .png) e
e .png) foi traçada uma reta secante à curva do gráfico, indicada por (s) com inclinação
foi traçada uma reta secante à curva do gráfico, indicada por (s) com inclinação .png) . O ponto
. O ponto .png) forma, com os pontos
forma, com os pontos .png) um triângulo retângulo. O lado
um triângulo retângulo. O lado .png) que é um dos catetos desse triângulo é denominado
que é um dos catetos desse triângulo é denominado .png) . Já o outro cateto, o lado
. Já o outro cateto, o lado .png) é denominado de
é denominado de .png) , pois representam variações em x e em y, respectivamente.
, pois representam variações em x e em y, respectivamente.
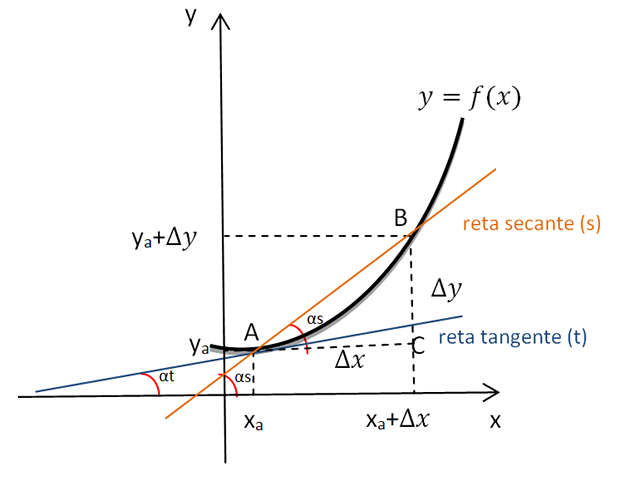
Quando o ponto .png) percorre a curva, tendendo para o ponto,
percorre a curva, tendendo para o ponto, .png) ,isto é, se aproximando cada vez mais, tanto quanto se queira, sem, no entanto chegar a
,isto é, se aproximando cada vez mais, tanto quanto se queira, sem, no entanto chegar a .png) , provoca as seguintes consequências:
, provoca as seguintes consequências:
- As diferenças
.png) e
e .png) tendem a zero:
tendem a zero: .png) .
. - A reta secante, indicada por (s) que passa pelos pontos
.png) ,tende a uma reta tangente, indicada por (t), com inclinação
,tende a uma reta tangente, indicada por (t), com inclinação .png) no ponto
no ponto .png) :
: - A inclinação
.png) da reta secante tende à inclinação
da reta secante tende à inclinação .png) da reta tangente:
da reta tangente: .png)
No triângulo ABC, retângulo em C, marcamos o ângulo .png) . Calculando-se a tangente trigonométrica desse ângulo, temos
. Calculando-se a tangente trigonométrica desse ângulo, temos .png) .Esta relação entre os acréscimos é chamada de Função Razão Incremental.
.Esta relação entre os acréscimos é chamada de Função Razão Incremental.
Levando-se ao limite da Função Razão Incremental, quando o acréscimo dado à variável independente tende a zero, obtém-se a derivada da função .png) .
.
Em linguagem matemática, vem:
.png)
Usam-se os símbolos .png) para se indicar a derivada de uma função, na variável dependente y, em relação à variável independente x. Ou de forma mais simples: a derivada de y em relação à x.
para se indicar a derivada de uma função, na variável dependente y, em relação à variável independente x. Ou de forma mais simples: a derivada de y em relação à x.
Como, de forma geral, .png) e
e .png) ,ou seja, as diferenças entre valores finais e iniciais, a definição de derivada também pode ser escrita assim:
,ou seja, as diferenças entre valores finais e iniciais, a definição de derivada também pode ser escrita assim:
.png)
E a derivada de uma função .png) em um ponto específico
em um ponto específico .png) é definida por
é definida por
.png)
Exemplos:
Ex1. Calcule pela definição a derivada da função .png) .
.
Solução:
Primeiro, damos acréscimos às variáveis x e y:
.png)
Isolando .png) , vem que
, vem que
.png)
Substituindo y:
.png)
Dividindo ambos os termos por, .png) tem-se que
tem-se que
.png)
Levando-se ao limite, quando
Pode-se, também, resolver este exercício usando diretamente a definição:
.png)
Solução:
.png)
Substituindo no limite, temos:
.png)
Ex2. Calcule a derivada da função .png) no ponto de abscissa
no ponto de abscissa .png) .
.
Solução:
Usando a expressão. .png) , vem que:
, vem que:
.png)
Mais adiante, estudaremos qual é o significado geométrico de se calcular uma derivada em um ponto específico.
Ex3. Usando a definição de derivada, derive a função .png)
Solução:
.png)
Substituindo no limite, vem que:
.png)
Ex4. O mesmo para a função .png)
Solução:
.png)
Substituindo no limite, vem que:
.png)