Derivadas das Funções na Forma Paramétrica
É comum expressar as funções com uma variável em função de outra. Em muitos casos, torna-se muito conveniente que as ambas as variáveis sejam expressas em função de uma terceira variável chamada parâmetro. Geralmente, usa-se a letra “t” para indicarmos esse parâmetro.
Se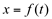 
e 
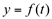variam dentro de um intervalo de valores de 
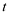, então o conjunto de pontos tal que 
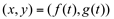define uma curva parametrizada. Essas equações são chamadas de equações paramétricas dessa curva.
Exemplificando, a equação de uma circunferência de centro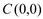 
e raio 
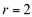é expressa em sua forma cartesiana por 
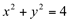. Esta mesma equação pode ser escrita na forma paramétrica da seguinte maneira:
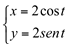, com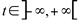 
. Isto significa que quanto t varia com os infinitos valores do intervalo, faz com que descreva todos os pontos x e y da circunferência.
Para calcularmos a derivada de uma função, na forma paramétrica, usamos a seguinte fórmula:
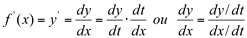
Ex4. Dada a função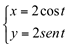 
, determine 
.
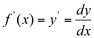Solução:
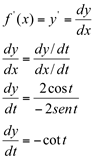
Esta derivada também pode ser escrita na forma cartesiana. Para isto, fazemos alguns artifícios de cálculos:
Tomando a equação na forma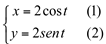 
Dividindo-se, membro a membro, a equação (1) por (2), vem que: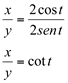
Substituindo-se na derivada, temos que: